前一頁
回目錄
科學時代——數學——不可秤量的流体——單位——原子論——電流——化學效應——電流的其他性質——光的波動說——電磁感應——電磁力場——電磁單位——熱与能量不滅——气体運動說——熱力學--光譜分析——電波——化學作用——溶液理論
科學時代
如果我們有正當的理由把十九世紀看做是科學時代的開始的話,那么,原因并不僅僅在于,甚至主要不在于,我們對自然的認識在十九世紀中有了迅速的發展。自有人類以來,人們就在研究自然:原始的生活技術就是對物性的片段知識的運用,早期的神話与寓言就是根据當時已有的證据創立的世界和人類起源的理論。但在最近一百年或一百五十年中,人們對于自然的宇宙的整個觀念改變了,因為我們認識到人類与其周圍的世界,一樣服從相同的物理定律与過程,不能与世界分開來考慮,而觀察、歸納、演繹与實驗的科學方法,不但可應用于純科學原來的題材,而且在人類思想与行動的各种不同領域里差不多都可應用。
在以前時代的大發明中,我們看見實際生活的需要推動技術家取得進一步的成就:那就是說除了偶然發現所帶來的發明之外,需要常在發明之先。但在十九世紀里,我們就看見為了追求純粹的知識而進行的科學研究,開始走在實際的應用与發明的前面,并且啟發了實際的應用和發明。發明出現之后,又為科學研究与工業發展開辟了新的領域。例如,法拉第(Faraday)的電磁實驗促成了發電机和其他電磁机器的發明,這些發明又向科學家提出新問題并給予科學家解決這些問題的新力量。麥克斯韋對于電磁波的數學研究,五十年后帶來了無線電報与無線電話,這些技術又給物理學家提出了一些新的問題。巴斯德發現發酵、腐朽以及許多疾病都是由于微生物的作用以后,工業、醫藥与外科方面都取得了极重要的成果。孟德爾(Mendel)在布呂恩修道院里所進行的豌豆遺傳的實驗帶來了系統的植物栽培以及小麥和其他谷類的許多改良
品种,并且促使人們認識到某些有關動植物某些特性的遺傳的原理。這种知識在今后對人類的福利也許會產生不可計量的影響。總之,科學過去是躲在經驗技術的隱蔽角落辛勤工作,當它走到前面傳遞而且高舉火炬的時候,科學時代就可以說已經開始了。
本世紀所特有的各种思想有許多在十九世紀開始的時候就已存在了,因而要划出一個明确的歷史界限是不可能的。而且在技術科學的應用上,至今仍在進行的偉大工業革命,也早已開始了。在1769年瓦特得到冷凝器原理專利權的時候,工業革命的主要工具之一蒸汽机已經到了可以應用的階段。這是一個實用的發明,后來才應用科學的原理去改進它、發展它。但是,使得世界社會情況發生革命性變化的另一大發明:電報通信,卻是純粹科學研究的結果;這种研究的開端可以追溯到1786年伽伐尼(Galvani)的工作。反轉過來,為了便利海底電信而發明出來的反射鏡電流計,對于純科學也有很大的好處。
有些人看來,科學的實際應用,代表它的主要成就。但這些活動對人類思想的影響雖然很大,卻是間接、緩慢和積累的。人類控制物質資源的能力,逐漸地、顯然不可避免地擴大開來,主要是靠了應用科學,因此,在一般人眼里,應用科學的重要遠遠超過于純科學。事實上,在他們看來,科學的胜利一個接著一個,其結果,顯然進展縱然緩慢卻是所向無敵的。人類控制自然的能力的擴展似乎沒有止境;人們都毫無理由地認為擴大控制自然的能力所用的机械原理,足可以解釋整個宇宙的秘奧。
在我們要敘述的這一時期里,主要的傾向,是把動力學的實驗与數學方法逐漸推廣到物理學的其他學科中去,而且在可能的情形下,并應用到化學和生物學上去。科學的研究,至少在一時期里,和哲學探討分了家。在整個十九世紀里,多數科學家都有意識地或無意識地抱有一种常識性的見解,以為科學所揭示的物質、它的性質及其間的關系,就是終极的實在,而人的身体就是机械結构,也許偶爾為心靈所控制或影響。許多物理學家在考慮科學的基本概念時,認識到這些意見是便利工作的假設,經不起嚴格的考察;但在實驗室与實際生活中,人們卻沒有時間來從哲學的角度表示怀疑。
在牛頓与拉瓦錫所奠定的基礎上,物理學与化學建立起一座不斷發展与和諧一致的大廈。這個成就使人們感覺總的路線已經一勞永逸地規划好了,此后不會再有什么惊人的新發現了,剩下來的工作不過是把科學的度量弄得更加精密,把几個明顯的空隙加以填補罷了。事實上,這就是十九世紀末革命性發展前夕以前人們的信念。
數學
在十九世紀里,出現了許多數學的新科目。其中我們必須提到數論、形論与群論,三角學發展成為多重周期的函數理論,以及一般的函數論。綜合与分析的方法創造出一种新的几何學,而許多這樣的方法被應用到物理學問題上去,這可能就是后來引導物理科學大踏步前進的推動力中最大的推動力。
數學史的細節不在本書范圍之內,這里只想談談對物理學主要部門具有特別重要性的几個數學分支的輪廓。
傅立葉(Fourier)在1822年出版的討論熱傳導理論的《熱的分析理論》一書里,證明一個變數的函數,無論是否連續,都可以展開為那個變數的倍數的正弦級數;這個結果后來被應用到珀松(Poisson)所提出的分析方法上去。高斯(Gauss)發展了拉格朗日和拉普拉斯的研究成果,并把這种成果應用到電學上去。他并且建立了量度誤差的理論。
拉格朗日列出運動的微分方程式,使動力學得到极大的進步,哈密頓(William Rowan Hamilton,1805-1865年)爵士又把這個工作推進了一步。哈密頓用一個系統中的動量与坐標去表示動能,并發現怎樣把拉格朗日方程式轉化為一組一階微分方程式去決定運動。他還發明了四元數。
薩卡里(Saccheri)在1733年,洛巴捷夫斯基(Lobatchewski)在1825年和1840年,高斯在1831年和1846年,波約(Bolyai)在1832年分別對歐几里得几何學所依据的一些假定進行了討論。1854年,黎曼(Riemann)促使人們普遍注意到非歐几里得几何學,以后凱利(Cayley)、貝爾特腊米(Beltrami)、赫爾姆霍茨(Helmholtz)、克萊因(Klein),怀德海等又做了不少工作。這些作者都指出,我們可以在數學上討論非歐几里得空間的性質,不管這樣的空間是否為感官所認識這個問題有怎樣的答案。到愛因斯坦建立了現代的相對性理論的時候,他們的研究才在物理學上變得很重要。
不可秤量的流体
熱的強度的概念是從人們的感官知覺而來的,溫度計幫助我們去測量它。阿蒙頓(Amon-tons)利用水銀改進了早期的溫度計,華倫海特(Fahrenheit)、列奧彌爾(Reaumur)与攝爾絮斯(Celsius)各自确立了標度。熱的傳播及輻射、對流和傳導三者的區別,以及熱量的概念,都是后來的研究課題。雖然最敏銳的自然哲學家,如牛頓、波義耳与卡文迪什等傾向于認為熱是物体質點的顫動,但在還沒有同我們的能量觀念相當的确定概念以前,他們的意見是不能發展的。要前進一步就需要把熱看做是一种可測度的量,由一物体傳到另一物体時,數量仍然維持不變。在這個觀念的指導下去進行實驗,就需要對熱的性質給予确定而适合的表述。于是就有一种學說應運而起。這一學說認為熱是微妙的,既不可見而又無重量的流体,在物体的質點間极其自由地流通。
布萊克(Joseph Black,1728-1799年)澄清了把熱和溫度兩种概念混淆起來的看法,分別稱之為熱的分量与強度。他從蒸餾酒厂得到啟發,研究了冰融為水及水化為汽的狀態變化。他發現在這些變化里大量的熱被吸收,而溫度卻不改變。他說這些熱成了“潛熱”。他以為熱流体或“熱質”与冰結合而成水,成為“准化合物”,熱質再与水化合而成汽。他的量度說明,融解一定量的冰為水所需的熱量与把同量的水加熱到華氏140度所需的熱量相等,但真正的數字是華氏143度。他還低估了汽化的潛熱,把967度F誤為810度。但這种測量要十分精确是很難的。布萊克又創立了比熱的理論來解釋為什么使不同物質發生相同的溫度變化所需的熱量是不同的,后來他的學生伊爾文(Irvine)詳細地測定了一些物質的比熱。這樣他就創立了熱量測定的方法,即量熱術。熱質說或熱的流体說一直引導科學前進,到1840至1850年間,赫爾姆霍茨与焦耳才證明熱動等价,确立了熱是運動的一种方式的觀念。
另一類似的流体說,或者說敵對的兩流体說,引導了電的現象的研究者前進。要解釋由于摩擦而帶電的兩個物体為什么彼此相引或相斥,可以假定電是与熱相似的一种物質,是一种可加減的量。但在電的早期歷史中,我們清楚地認識到有兩种不同而且相反的電。玻璃与絲摩擦所生的電,可被硬橡膠与毛皮摩擦所生的電中和。為了解釋這些結果,流体說假設有兩种性質相反的流体或者有一种流体,它在比常量多或少時,就引起帶電的狀態。我們現在還在使用正電、負電等适合于單流質說的許多術語,雖然我們已經知道電不是連續的流体而是微粒的結构,這是我們在后面要說明的。當人們用起電机產生出比較大量的電,再貯蓄在來頓瓶(一個內外都貼上錫箔的玻璃瓶)一類電容器中的時候,就給實驗帶來很大方便。格雷(Stephen Gray,1729年)、杜費伊(du Fay,1733年)与普利斯特列(Priestley,1767年)首先分清了導電体与絕緣体,這兩術語則是德扎古利埃(Desaguliers,1740年)所定出的。
人們一注意到電瓶放電的火花与聲響,也就馬上認識到它們与雷電相似,因而也就疑心這兩种現象性質一樣。怎樣才能證明兩行性質相同呢?怎樣才能使天上的雷公服從物理學定律呢?富蘭克休(Benjamin Franklin,1706-1790年)對這個問題似乎入了迷。他留下的許多信札里都描繪了不少來頓瓶放電的實驗,并提到天電有熔化金屬、撕破物質等效應。
在帶電体尖端的放電作用的啟發下,達利巴德(d’Alibard)与其他法國人產生了把閃電傳導下來的念頭。1752年,他們在馬里地方裝置了一根高40呎的鐵竿,要“決定帶有閃電的云是否帶電的問題”。當電云在竿上經過時,竿下端即發生火花。這個實驗在其他國家也重复做過,而且完全成功——事實上,圣彼得堡的里曼(Riehmann)教授竟因為在屋上裝置鐵竿引導雷電而當場被擊斃!同時富蘭克林則用風箏安全地進行了同樣的實驗。
在風箏主杆的頂端裝上一根很尖的鐵絲,約比風箏的木架高出一呎余。在麻繩的下端与手接近之處系上一根絲帶,絲帶与麻繩連接之處可系一把鑰匙。當雷雨要來的時候,把風箏放出,執繩的人必須站在門或窗內,或在什么遮蔽下,免使絲帶潮濕;同時須注意不讓麻繩碰到門或窗的格子。雷云一經過風箏的上空,尖的鐵絲就可從雷云吸引電火,使風箏和整根麻繩帶電,麻繩另一端的纖維都向四周張開,若將手指接近,就會被其吸引。當風箏与麻繩都被雨濕,而能自由傳導電火時,你若將手指接近,便會看見大量的電由鑰匙流出。從這把鑰匙那里可以給小瓶蓄電;由此得來的電火可使酒精燃燒,并用來進行別的有關電的實驗;而這些實驗平常是靠摩擦小球或小管來做的,這樣就完全證明這种電的物質和天空的閃電是同樣的。
十八世紀時,人們進行了許多次加熱于電气石等礦石与晶体而生電的實驗,而且電鰻一類電魚能給人以麻痹性打擊的現象,也再度引起人們的注意。有人考察了它們的電器官,弄清它們給予人的打擊的确是由于電的現象所致。
電力和磁力的研究開始于十八世紀末年。米歇爾和法國軍事工程師庫侖(Coulomb)先后在1750年左右和1784年發明了所謂扭秤,即一條輕的水平鐵片,在中點上系上一根長鐵絲,挂在一個玻璃匣內。庫侖把一個帶電的球放在鐵片的一端,再拿一個帶電的球与它接近,這鐵片即會扭轉。他又拿一塊磁鐵換替鐵片,再用另一磁鐵和它接近也可使磁鐵的一极扭轉。他用這個方法發現電力和磁力都隨著距离平方的增加而減少,證明這些力量和牛頓證明的引力有同樣的關系。他還發現電力与電荷量成正比,因而可以用電力來量度電荷。這個有關電力的定律還先后由普利斯特列和卡文迪什用另外的方法發現過。他們用實驗證明任何形狀的閉合帶電導体里面都沒有電力,所以球体內也沒有電。牛頓過去用數學方法證明,如果平方反比的定律有效,一個由具有引力的物質构成的均勻球殼對于其內部的一個物体沒有力的作用,而且任何別的力的定律都不會有這個結果;同樣的研究也适用于電力。
力的定律既然成立,數學家就把靜電學的課題拿過去,導出一系列周密的關系,在可以与觀察結果比較的情況下,都證明与觀察結果完全符合。導体表面電荷的分布,導体附近的電力与電位,導体与絕緣体的各种排列的電容量等,在高斯、珀松与格林的巧妙的手中,都證明可以用數學方法處理。
電是一种無重量、不可壓縮的流体的學說和電是一個确定的量的觀念是一致的,雖然在研究上并不是必不可少的,事實上卻提出一個便于說明和研究這些現象的方便的畫面。
更有歷史意義的是人們的注意轉向電力。与引力相同,電似乎也越過空間而作用于遠處。數學家看來這不需要進一步的解釋,但物理學家很快就開始推測這個空間的性質。因為這個空間竟然能傳播兩种表面上不同的力。我們以后會知道,這就引起了現今叫做“場物理學”的現代理論。
單位
重量与度量單位繁多,人們過去就感到十分不方便,至今仍然如此。法國人首先創立了合邏輯的、方便的十進制來代替這些繁多的單位。1791年,法國國民議會接受了一份專門委員會的報告,1799年完成了必需的量度標准,并決定采用;1812年決定自由使用,1820年強迫施行。
長度的基本單位是米,原來定為通過巴黎的地球經圈一象限的一千万分之一。但實際上,一米的長是等于攝氏零度時某一條金屬棒兩點間的距离。后來大地測量的精确度增高,知道米長并不恰好等于地球的經圈的一個象限的若干整分,但不加以改正。容量的單位是立特或升,應當是每邊一分米(1/10米)的立方体,但以其不易量度,1901年規定為一公斤(千克)的純水在一大气壓及攝氏四度(在這溫度下水的密度最大)下的容積。
質量的單位是千克或公斤,原來規定為每邊一分米的純水在攝氏四度下的質量,但現在則等于1799年勒費貝-紀諾(Lefebre-Ginneau)与法布隆尼(Fabbroni)所制定的鉑銥合金標准衡器的質量。他們的工作的精确度可從吉洛姆(Guillaume)在1927年所定的最新立特值去判斷,即一立特之值等于1000.028立方厘米。
時間的單位是砂,定為平均太陽日的1/86400,所謂平均太陽日是把太陽中心第一次過子午線和接連第二次過子午線之間的時間作為一年計算出來的平均時間。
1822年,傅立葉在他的《熱的理論》里指出副量或導來量按基本量來表示時,有某些是綱。假設以L表長度,M表質量,T表時間,則速度u(即在單位時間內所經過的長度)的量綱為L/T或LT-1。加速度是單位時間內速度的變化,其量綱為v/T,即L/T2或LT-2。力是質量与加速度的乘積,或MLT-2;功是ML2T-2。高斯由這些動力單位導出電与磁的單位,以后還要提到。
約在1870年,達成一項國際協議,一致同意采用一項科學的量度系統,以厘米(1/100米)、克(1/1000公斤)和秒三者作為基本單位,這就是常說的厘米、克、秒(C.G.S)制。
原子論
前几章內,我們已將德謨克利特時代以來的原子哲學敘述過了。這個哲學經亞里斯多德駁斥后,在中世紀陷于停止狀態,直到文藝复興以后,才重新活躍起來。伽利略贊同這個哲學,伽桑狄用伊壁鳩魯与盧克萊修的語言重新加以敘述;波義耳与牛頓在他們關于化學与物理學的思辨見解中也用了它。從那時以后它又被擱置,雖然它仍然滲透在科學思想中。
到了十九世紀初年,它被人重新提出,以解釋固、液、气物質三態的物理性質,以及化學變化上的定量事實。
推翻燃素說以后,人們對物質的三態或三相有了更清楚的認識。物質雖然有三態,我們通常認識最清楚的總是其中一態,如我們認識最清楚的水經常是液体;但水可變為三態中的任何一態,如冷凝則為冰,蒸發則為汽。隨著這种認識的進步,人們開始研究化學化合定律。气体的化合定律,最容易發現,因此,气体就不再是一种神秘的、半靈魂的實体,而与其他物体發生關系了。
根据精密分析的結果,人們,尤其是拉瓦錫、普魯斯特(Proust)与李希特(Richter)等發現一個化合物始終絲毫不差地由同量的成分所組成(在當時達到的精度下),這個定量化合的觀念,在新化學的体系中起了重要作用,雖然它和貝爾托萊(Berthollet)的有分量的見解是不相合的。水不論是怎樣得來的,總是氫与氧按1与8的比例而合成的。因此我們得到化合重的觀念,如以氫的化合重為1,則氧的化合重為8。兩种元素以多种方式化合成多种化合物時,一化合物中兩种成分的比例与另一化合物中兩种成分的比例,常有簡單的關系:在一化合物中14分氮与8分氧化合,在另一化合物中則与16分氧化合,恰為前者的兩倍。可是在同位素發現后,這种定量化合的概念稍有改變,以后還要談到。
約翰·道爾頓(J.Dalton,1766-1844年)是威斯特摩蘭(West morland)一個手机織工的儿子,在他做小學教員的稀少閒暇里,學得一些數學与物理學的知識。他在曼徹斯特得著一個教書的位置,開始他對气体的實驗。他看到气体的性質最好用原子論去解釋,后來他把這种觀念應用到化學上去,指出可以把化合的現象解釋為具有确定重量的相异質點的結合,而每一元素的質點都有其特定的重量。他說:
物体有三种不同的區分或三態,特別引起哲學的化學家的注意,即彈性流体、液体与固体三詞所代表的狀態;我們所熟悉的很有名的例子是水,它在某些情況下,可以具有三种狀態。在蒸汽,我們看見它是完全彈性的流体,在水,是完全的液体,在冰,是完全的固体。這些觀察結果默默地引到一個似乎得到公認的結論:凡有相當大小的物体,不管它是液体式固体,都是由無數极微小的質點或原子所組成,他們為一种引力所束縛,這种引力因情況不同而有強弱的差异。……
化學的分解与合成不過是把這些質點分開或聯合。物質的新創或毀滅是不在化學作用的能力范圍之內的。我們要想創造或毀滅一個氫的質點,和在太陽系里增加一顆新的、或毀滅一顆固有的行星,一樣的不可能。我們所能做到的改變,只是把粘著狀態下或化合狀態下的質點分開,以及把原來分离的質點聯合起來而已。
在一切化學研究里,人們都正确地認為,弄清化合物中簡單成分的相對重量,是一個重要的目標。不過,不幸的是,過去化學的研究就停止在這里;人們本來很可以從物質的相對重量,推出物体的終极質點或原子的相對重量,由此看出,它們在各种其他化合物中的數目与重量,用來幫助和指導我們未來的研究和改正研究的結果。因此,本書的一個重大目標,就是說明測定下列几個量的重要性和好處:單体与化合物中終极質點的相對重量,組成一個复雜質點的簡單基本質點的數目,參与构成一個較复雜質點的比較不复雜的質點的數目。
如果有A与B兩個可以化合的物体,以下為從最簡的化合開始的各种化合的可能次序,有:
A的1原子+B的1原子=C的1原子,二元的。
A的1原子+B的2原子=D的1原子,三元的。
A的2原子+B的1原子=E的1原子,三元的。
A的1原子+B的3原子=F的1原子,四元的。
A的3原子+B的1原子=G的1原子,四元的。
我們可以采取以下的通則,作為一切關于化學化合的研究的指針:
1.如果兩物体化合時只得出一种化合物,我們必須假定這种化合是二元的,除非有某种造成相反情況的原因出現。
2.如果發現有兩种化合物,則必須假定它們一個是二元的,一個是三元的。
3.如果有三种化合物,則可預料一個是二元的,其他兩個是三元的……等等。
把這些規則應用到已經查明的化學事實上去,我們得到以下的結論:1.水是氫与氧的二元化合物,這兩种元素的原子的相對重量約為1:7;2.氨是氫与氮的工元化合物,這兩种元素的原子的相對重量約為1:5;3.氧化氮的气体是氮与氧的二元化合物,它們的原子重量為5与7;4.氧化碳是由一個碳原子与一個氧原子构成的二元化合物,共重約為12;碳酸气是三元化合物(有時也是二元的),它有一個碳原子和兩個氧原子,共重為19;等等。以上各种情形,都是以氫元素的原子為單位來表達其他元素的重量。
道爾頓的敘述,自然包含著當時難免的錯誤:例如他將熱看做是一种微妙的流体;他的化合重量也不精确,如以氫為單位時,氧的重量應該是8,而他定為7。他假定,如兩种元素的化合物只有一种,便應看做是一個原子与另一個原子的結合。這种假定也不是普遍适用的,因此,他對于水和氨的結构才有錯誤的觀念。雖然這樣,道爾頓把模糊的假說變成了确定的科學理論,的确取得科學史上的重大進步之一。
道爾頓在小圓圈中加上點、星和十字等記號來代表元素的原子。這個方法后來為瑞典化學家柏采留斯(Berzelius,1779-1848年)加以改進,形成我們現今所用的体系,即用字母為符號去代表同一個元素的原子量相當的該元素的相對質量。例如H不是模糊地代表氫元素,而是代表等于1(1克、1磅或其他單位)的氫的質量;O代表等于同一單位的16倍的氧元素的質量。
柏采留斯的主要實驗工作,是在當時可能范圍內,用最大的精确度來測定原子量,或者說等价的化合曼。他也發現了几個新元素,研究過許多化合物,更在礦物學的研究上,揭開了一個新的篇章。他与戴維(Davy)聯合确立了電化學的基本定律,并且看到電极性与化學余合力之間的密切關系。他把這觀念推廣得太遠,而為當時所難了解:他認為一切原子都含有陽電或陰電由于其相對力量,它們才化合。他認為每一化合物都是帶异性電的兩部分所組成。如果几個化合物互相化合,我們可以設想那是由于多余的异性電荷的作用。這個二元論的理論不夠應付日益增進的知識,到有机化學興盛時,就為基型說所代替了。現在我們明白化學和電兩种現象有密切的關系,不過不如柏采留斯所想象的那樣簡單。
當人們對气体化合現象加以更廣泛的研究時,道爾頓原來的原子觀念,便表現出有缺陷。蓋伊-呂薩克(Gay-Lussac,1778-1850年)表明气体化合時,其容積常有一定的簡單比例,阿伏伽德羅伯爵(1776-1856年)在1813年指出:根据道爾頓的理論,和蓋伊-呂薩克的觀測,我們可以推斷一切同容積的气体所含的原子數,必定彼此有簡單的比例。安培于1814年獨立得到相同的結論,但被人忘記或忽視了,到1858年,坎尼查羅(Cannizzaro)才再度澄清了這個問題。到那時,人們才從气体化合的事實以及從物理學的考慮看出,有必要把化學上的原子和物理學上的分子區別開來。化學上的原子是物質參加化合的最小部分;物理學上的分子,是能自由存在的最小質點。表達阿伏伽德羅假設的最簡單方法,是假定同容積的气体含有同數的分子。以后我們還要說明這結果可用數學方法從物理學上的一個理論推導出來,這個理論假定气体的壓力是由于它的分子常在不斷地運動和碰撞而產生的。
但回到水的問題來,二容積(即二分子)的氫与一容積的氧化合,而得二容積(或二分子)的水汽。解釋這些關系最簡單的理論,是假定物理學上的氫分子与氧分子,每一分子都含兩個化學原子,而水汽分子具有可以用H2O代表的化學結构,因而這變化可以下列方程式去表示:
2H2+O2=2H2O
(2容積)(1容積)(2容積)
這樣,既然氧的化合量是8,而一個氧原子可以和兩個氫原子化合,如果取氫的原子量為單位,則氧的原子量應是16而非8。所以在決定各元素的原子量以前,我們必須將道爾頓的化合量加以調整,使之合于后來實驗所發現的事實。首先按照所有證据系統地進行了這番工作的就是坎尼查羅。
由于一個氧原子和兩個氫原子化合,我們就說氧的原子价是2。原子价的觀念,是以后許多年間大部分化學思想的基礎。
已知的元素已經由道爾頓所認識的二十個增加到現在的九十多個。元素發現的工作,是夜間歇不定中進行的。當一個新的研究方法應用到化學問題的時候,就常常會發現一串新元素。電流的分解力使戴維爵士(1778-1829年)在1807年分离出鹼金屬的鉀与納。稍后光譜分析使我們發現銣、銫、鉈、鎵等物質。放射性的方法使我們發現了鐳和它同族一類元素,阿斯頓的攝譜儀又使我們發現了許多同位的元素。
1815年,普勞特(Prout)就已經在研究元素的原子量与其物理性質之間的關系,隨后紐蘭茲(Newlands)与德·肖庫土瓦(deChaucourtois)也研究了這個問題。1869年,邁耶爾(Lothar Meyer)与俄國化學家門得列耶夫(Mendeleeff,1834-1907年)成功地證實了這种關系。門得列耶夫把元素按其原子量的順序,由輕到重排成一個表時,發現它們有一种周期性——象紐蘭茲所指出過的那樣,每第八個元素都有一些相同的性質,一切元素可以照這樣排成一表,使同性質的元素歸到一欄里去。利用這樣制成的周期表,可以把正确的原子量給与原子价未定的元素,表中的空白由門得列耶夫根据假設加以填補,這樣他就預言了一些未知元素的存在及其性質,其中一些后來竟被人發現了。
門得列耶夫認為他的周期表只是純粹經驗事實的敘述。但這樣的關系卻下可避免地使人回到物質有共同基礎的老觀念上去。許多人以為這個共同基礎可能就是氫,他們想證明如以氫的原子量為單位,其他元素的原子量全都是整數。雖然許多元素的原子量接近整數,但有几個元素,例如氯(CI=35.45)頑固地不遵從這個方案,斯塔斯(Stas)等人增加測定原子量的精确度以后,也不能消除這個偏差。要證明物質具有共同基礎并把原子量歸結為整數,還得等候半個世紀;這种工作是當時的實驗和理論能力辦不到的。
電流
我們在上面敘述的各种類型的起電儀器,都主要是用來把靜電荷賦予某种絕緣体的。的确,如果使起電机接地,形成一個導電通路,則在這電路中就有一點電流通過。不過,就是在最优良的摩擦起電机中,每一秒鐘通過的電量也都非常之少,以致要想在這電路上發現電流,那是很困難的,雖然,如果在導線中留一個空气間隙,則這起電机所生的高電位差,可以產生可見的火花。
十九世紀初,伽伐尼或伏特電池的發明,開辟了一個新的研究領域。這种電池引起了一系列現象,最初,稱為伽伐尼流,經過許多人的努力,慢慢地和另外一系列以電得名的現象聯系起來。我們終于明白所謂伽伐尼流,正是電的流動,只是和起電机所生的電量比起來,大很多,但其電位差卻比電机所生的電位差小得不計其數。由于在電路的任何一點上都不能發現積存的電,我們也不妨把電流比做一种不可壓縮的流体在不可伸長的剛性管內的流動。
伏特電池是由于偶然的觀察而發現的。這個發現,最初似乎要引到另外一個方向去。1786年左右,意大利人伽伐尼發現蛙腿在起電机的放電的影響下發生收縮。在這次觀察之后,他又發現:如果使神經和肌肉同兩种不相類似的金屬連接起來,而使金屬互相接触,也可以得到同樣的收縮。伽伐尼把這些效果歸因于所謂“動物電”;后來,另外一個意大利人帕維亞的伏特(Voita of Pavia)出來,證明這种基本現象并不依賴于一种動物物質的存在。1800年,伏特發明了以他的姓得名的電池。在十九世紀初年,這种電池成為一种研究的工具,在伏特和他的同時代的別國人手中,產生了一些很有趣味的結果。當時的科學雜志登滿了奇异的新發現的消息。當時的人都用极大的熱情去研究這些發現,其熱烈的程度,不亞于一世紀以后,人們闡釋气体中的放電与放射現象時,所表現出的那种熱忱。
伏特所制的電池,是用一串鋅盤、銅盤以及為水或鹽水浸濕的紙張,按下列次序相疊而成的:鋅,銅,紙,鋅,如此類推……最后是一個銅盤。這樣一种組合,其實就是一個原始的原電池組。每一對小盤為浸濕的紙隔開,而成一個電池,造成少許電位差。這些小電池的電位差加在一起,便成了電池組銅鋅兩端的相當大的總電位差(或不恰當地叫做電動力)。另一种裝置法是把若干裝有鹽水或稀酸的杯子集合在一起,每個杯子裝置一塊鋅片和一塊銅片。前一杯子的鋅片与次一杯子的銅片相聯,這樣一直繼續下去,留下最先一個鋅片和最后一個銅片,作為電池組的兩极。伏特以為效果的來源在金屬的聯接處;因此圓盤和兩极的金屬片的次序才如以上所述。這些金屬片或圓盤不久便發現是無用的,雖然它們在這种儀器的早期圖畫中占有重要地位。
如果我們從伏特的電池取用電流,其強度便迅速地衰減,主要由于銅片的表面上生了一層氫气膜。這种電极化,可用硫酸銅溶液圍繞銅片來阻止,這樣生成的物質是銅而非氫;或用碳棒代替銅片,把它放在氧化劑如硝酸或重鉛酸鉀的溶液中,這樣所產生的氫气就立刻變為水。
化學效應
當伏特的發現的消息在1800年傳到英國時,立刻就有人進行廣一些基本觀察,促成了電化學的誕生。尼科爾森(Nicholson)与卡萊爾(Carlisle)在把伏特電池的原來裝置加以改變時發現:如果用兩條黃銅絲連結電池的兩极,再將兩線的他端浸在水中,并使其互相接近,一端有氫气發生,另一端的黃銅線被氧化。如用白金絲或黃金絲來代替黃銅絲,則不發生氧化,氧以气体狀態出現。他們注意到氫气的容積約為氧气的二倍,這正是氫氧二气化合成水的比例。他們說明這种現象就是水的分解。他們還注意到使用原來的裝置時,電池內也有類似的化學反應。
不久,克魯克香克(Cruichshank)分解了氯化鎂、碳酸鈉(蘇打)和氨(阿摩尼亞)溶液,并且從銀和銅的溶液中,將這些金屬沉淀出來。這一結果以后導致電鍍的方法。他又發現在陽极周圍的液体變成鹼性,而陰极周圍的液体變成酸性。
1806年,戴維爵士(1778-1829年)證明酸与鹼的形成是由于水中的雜質的緣故。他在以前已經證明,即使將電极放在兩個林中,水的分解也可進行,但須用植物或動物材料將兩個杯子聯接起來。同時他還證明電效應与電池內化學變化有密切關系。
伏特認為伽伐尼現象与電是同一現象。這個問題成了許多人研究的題目。到1801年,沃拉斯頓(Wollaston)證明兩者發生相同的效果之后,才确定兩者确是同一現象。1802年,埃爾曼(Erman)使用驗電器測量了伏特電池所提供的電位差。這時,才明白老現象表現“緊張中的電”,而新現象表現“運動中的電”。
按照公認的慣例,我們一致同意假定電向所謂正電方向流動,即在電池內由鋅版流到銅版(或碳棒),在電池外沿著導線由銅流到鋅。根据這個慣例,銅版稱為電池的正段,而鋅版稱為負极。
1804年希辛格爾(Nisinger)与柏采留斯宣布中性鹽溶液可用電流分解,酸基出現于一极,金屬出現于另一极,因而他們斷定:新生性的氫元素并不象以前所假想的那樣,是金屬從溶液中分离的原因。在當時所知道的金屬中,有許多都用這個方法制備出來了,1807年,戴維更分解了當時認為是元素的碳酸鉀与碳酸鈉。他讓強電流通過含水的這兩种物質,而分离出惊人的鉀与納金屬。戴維是康沃爾城(Cornwall)人,聰明、能干而又會講話,他做了那時新成立皇家學院的化學講師,他的講演趣味丰富,吸引了許多人士參加。
化學化合物可以用電的方法來分解,說明化學力与電力之間是有聯系的。戴維“提出一個假設,說化學的吸力与電的吸力同生于一因,前者作用在質點上,后者作用在質量上”。柏采留斯更將這看法加以發展。我們已經說過,他認為每個化合物都由帶相反的電的兩份結合而成,這帶電的部分可能是一個或一群原子。
一個可注意的事實是分解的產物只出現于兩极。早期的實驗者已經注意到這現象,并提出各种不同的解釋。1806年,格羅撤斯(Grotthus)設想這是由于溶液中的物質不斷地在那里分解与复合,在兩极間,互相鄰接的分子互換其相反的部分,在這條聯鏈的兩端,相反的原子就被釋放出來。
在電化學方面的最初發現以后,中間停頓了一個時期,到后來,大實驗家法拉第(Michael Faraday,1791-1867年)才重新拾起這問題來。法拉第是戴維在皇家學院實驗室的助手与繼承人。
1833年,法拉第在惠威爾的建議下,制定一套新名詞,至今還在使用。他不用pole(极)這個字,因為它含有相引相斥的陳舊觀念,而采用electrode(電极)(&&&s=路徑)一詞,將電流進入溶液的一端叫做anode(陽极),出來的一端叫做Cathode(陰极)。化合物的兩部分,循相反的方向在溶液中行動的,叫做ions(离子)(io=我去);走向陰极的叫cations(陰离子),走向陽极的叫ani-ons(陽离子)。他又用electrolysis(電解)(0。一分解)一詞來代表整個過程。
經過一系列的巧妙的實驗,法拉第將复雜的現象歸納成為兩個簡單的結論,即我們所說的法拉第定律。(1)不管電解質或電极的性質是什么,由電解所釋出之物的質量与電流強度及通電時間成比例,換句話說即与通過溶液的總電流量成比例。(2)一定量的流量所釋出之物的質量与這物質的化學當量成比例.即不与原子量,而与化合量成比例,亦即与原子价除原子量的數值成比例;例如釋放1克氫元素,必出現16+2即8克的氧元素。通過一單位電流所釋出之物的質量叫做該物質的電化當量。例如1安培的電流(即C.G.S.單位的1/10)通過酸溶液1秒鐘之后,即有1.044×10[-5]克的氫被釋出來,如用銀鹽溶液即有0.00118克銀分离出來。這樣分离出來的銀的重量很容易加以精确的秤量,所以后來竟把它作為電流的實用單位即安培的定義。
法拉第的定律似乎可以應用于一切電解情況;相同的一定電流量總是釋放出單位當量的物質。電解必須看做是游動的离子在液体中帶著相反的電到相反的方向去。每一离子帶一定量的正電或負電,到電极時就釋放离子,而失去電荷,只要電動力的強度可以胜過反對的极化力。后來赫爾姆霍茨說:法拉第的工作表明,“如果接受元素是由原子組成的假設,我們就不能不斷定:電也分成一定的單元,其作用正和電的原子一樣”。如此說來,法拉第的實驗不但成為理論電化學及應用電化學以后的發展的基礎,而且也是現代原子与電子科學的基礎。
電流的其他性質
雖然早期實驗者的注意主要集中在伽伐尼電流的化學效應上,他們也沒有忽視其他現象。不久他們便發現;當電流通過任何導線時,就有熱發生,多寡依照導線的性質而不同。這种熱效應在現今的電燈、取暖等方面,有极大的實用价值。另一方面,1822年,塞貝克(Seebeck)發現兩种不同金屬聯接成閉合線路時,在其接頭處加熱,便有電流發生。另外一個更有興趣的現象是:電流具有使磁針偏轉的力量。1820年,哥本哈根的奧斯特(Oersted)發現這一現象。他看見這效應穿過玻璃、金屬和其他非磁性的物質而達到磁針。他還認識到,他或他的翻譯者所謂的“電沖突”“形成圓圈”,按照我們現在的說法就是:在長而直的電流周圍有圓形的磁力線。
人們,特別是安培(Andre Marie Ampere,1775-1836年)立刻認識到奧斯特的觀察結果的重要性,安培指出,不但磁針受了電流周圍的力的作用,電流自己也互相發生作用。他用活動的線圈進行實驗,來研究這些力的定律,并据數學證明:一切觀察到的現象都符合以下的假設:每一長度為dl的電流元,必在其外面的一點上產生cdl sin O/r2的磁力,式內c表電流的強度,r是電流元与這一點之間的距离,O是r与電流方向之間的角度。這樣,由電流所生的力又歸結到平方反比的定律,因此就同万有引力及磁极間、電荷間的力一致了。這又是走向“場物理學”的另一步。
自然,這种電流元不能用實驗分离出來,但是按照安培的公式,將所有電流單元的效應都加合起來,我們就能計算出電流附近的磁場。
根据安培的公式,我們也能算出磁場內的電流所受的机械力。在空气中磁极強度m所造成的磁力為m/r2,所以m=cdl sin θ。在磁場H中。所受的机械力是Hm,所以在空气中安培的電流元所受的力為Hcdl sinθ。從這個公式計算實際電路上的机械力,不過是數學問題而已。
遠距通信是從眼睛看得見的信號開始的。散布鄉間的許多“烽火台”,是久已廢棄的信號崗位的遺跡。它們曾把拿破侖登陸的消息迅速地傳達到了倫敦。電方面的每一個新發現都促使人們提出一些使用電報通信的意見,但在安培把他研究電磁所得的結果加以應用以前,這些意見都沒有什么結果。在安培的成果發表以后,實際机器的發明与采用,就僅僅是机械師的技巧与金融界的信任問題了。
1827年左右,歐姆(Georg Simon ohm,1781-1854年)做出很多貢獻,幫助從電的現象中抽繹出几种能夠确切規定的量來。他用電流強度与電動力的觀念代替了當時流行的“電量”和“張力”等模棱的觀念。電動力一詞相當于靜電學中已經使用的“電位”。當張力或壓力很高的時候,要將電從一點運到他點,必需要較多的功,因此電位差或電動力可以定義為將一單位的電由一點搬到他點時為了反抗這個電力所作的功。
歐姆關于電的研究是以傅立葉關于熱傳導的研究(1800-1814年)為根据的。傅立葉假設熱流量与溫度的梯度成正比,然后用數學方法建立了熱傳導的定律。歐姆用電位代替溫度,用電代替熱,并且用實驗證明這些觀念的有用。他發現:如電流由伏特電池組或塞貝克溫差電偶流出,通過一根均勻的導線,其電位的降落率是一個常數。歐姆定律一般寫作:電流c与電動力E成比例,
c=kE=E/R,
式內k是一個常數,可名為傳導率,而其倒數1/k或R,稱為電阻。R只隨導体的性質、溫度与大小而异,它与導体的長度成正比,而与其橫剖面的面積成反比。這后一事實表明電流是在導体的全部質量中均勻地通過。后來發現,在很高遠的交流電的情形下,還須加一些修改。
經安培与歐姆的努力之后,電流的問題已經到了新物理學的重要階段,因為适當的基本量已經選出,并有了确定的意義,因而給數學上的發展奠定了堅固的基礎。
光的波動說
十九世紀初年,還有另外一個古老的觀念复活起來和确立起來,這便是光的波動說。我們說過:光的波動說在十七世紀只有胡克等人模糊主張過,后來惠更斯才給予它一個比較确定的形式。牛頓根据兩個理由加以揮斥。第一,它不能解釋物影,因為牛頓以為如果光是波動的話,光波也如聲波那樣,會繞過阻礙之物。第二,冰洲石的雙折射現象說明光線在不同的邊上有不同的性質,而在傳播方向上顫動的光波不能有這樣的差异。托馬斯·楊(ThomasYoung,1773-1829年)与弗雷內爾(Augustin Jean Fresnel,1788-1827年)對這個學說賦予近代形式,而克服了這兩個困難。不過有一件事是值得回憶的:牛頓以為薄膜的顏色說明光線里的微粒使以太中產生附從波。這個學說与現今用來解釋電子性質的理論,惊人地相似。
楊使一束极狹窄的白光通過屏上的兩個針孔,再把一個屏放在第一個屏后面。當穿過兩個針孔的光線在第二屏上互相重疊時,就有一串顏色鮮亮的光帶出現。這些光帶是由于從兩個針孔光源而來的同類光波互相干涉而形成的。如果一個光波到達第二屏所走的路程和另一光波的路程的相差數恰為波長的一半,則這一光波的峰与另一光波的谷就恰好相遇,結果就產生黑暗。如果兩個光波前進的路程恰恰相等,兩者的波峰就恰好相遇,光亮也就加倍。我們實際所看見的光是由白光除掉一個波長的光所留下的多色光。如果我們不用多色混成的白光,而用單色光作實驗,則所得的將是明暗相間而非彩色的光帶。
由所用的儀器的尺寸以及光帶的寬度,我們可以計算出各种單色光的波長。這些波長經證明是非常之短,其數量級為一時的五万分之一,或一毫米的二千分之一,和牛頓認為易反射和易透射的間歇長度恰相符合。由此可見,在光線的路徑中,一般障礙物的大小比光波的長度大得很多,而且數學上的研究證明,如果我們假定一個前進的波陣面分解為無數同心圈,都環繞著与人目最接近的波陣面上的一點,那么,除了挨近那一點的同心圈之外,其余的同心圈必因干涉而相消,因而我們眼睛所看見的只有沿著直線而來的光。這樣,光差不多只沿直線進行,遇著障礙物而彎曲的現象只限于微小的衍射效應。
牛頓的第二困難為弗雷內爾所克服。胡克偶爾提到光波的顫動,可能与光線的方向相正交,弗雷內爾指出這個提示說明一線光在各方向上可能有不同的性質。如果我們看看一個前進光的波陣面,它的線性顫動非上下的即左右的。這樣的線顫動應產生所謂平面偏振光。如果一塊晶体在一位置上只能讓一個方向的顫動通過,第二塊同樣的晶体沿著晶軸旋轉90度之后,必將通過第一晶体而來的光完全遮斷。這正是光線通過冰晶石的現象。
弗雷內爾利用數學將光的波動說發展到很圓滿的境界。雖然還有一些困難,但大体說來,他的完善的學說与觀測到的事實异常符合。他和他以后的人如格林、麥克卡拉(MacCullagh)柯西(Cauchy)、斯托克斯(Stokes)、格萊茲布魯克(Glazebrook)等人經歷一個世紀,才把古典的光的波動說确立起來。
如果光波是与其前進的方向成正交的,則其媒質必須具有使這樣的波能在其中傳播的結构。气体与液体都不能具有這种結构。因此,如果光是机械式的波動,則傳光的以太必定有与固体類似的性質:即它必定帶有剛性。這就是把以太看做是有彈性的固体的許多學說的開端。怎樣才能把光的媒質所必需的這种性質和行星的運動沒有遇到可觀的阻力的事實調和起來呢?十九世紀頭七十年的許多聰明物理學家為此絞盡了腦汁。為了解釋這种必要的剛性,后來甚至有人設想以太具有回轉儀式的旋轉運動。
正如愛因斯坦所指出的,光的波動說的成功,在牛頓物理學中打開了第一道缺口,雖然當時沒人知道這個事實。牛頓把光看做是在空間中運行的微粒的學說,和他的別的哲學很相配合,可是這些微粒為什么只以一個不變的速度運動,很難了解。但等到人們開始把光看做是波動的時候,再要相信一切實在的東西都是由在絕對空間里運動的微粒所組成的,就已經不可能了。以太是為了保存机械觀點而臆造出來的,只要可以把光看做是在類似剛体的煤質中傳播的机械波動,以太就完成了這個任務,可是,如果假定以太無所不在,它已經在某种意義上与空間本身合而為一了。但法拉第指出空間也有電和磁的性質,到麥克斯韋證明光是電磁波時,以太就不必一定是机械的了。
光的波動說揭開了現今所謂場物理學的第一章。由法拉第和麥克斯韋的工作寫成第二章,把光与電磁聯系起來。在第三章里,愛因斯坦用几何學來解釋万有引力。也許有一天,万有引力可能和光与電磁波在更大的綜合里聯系起來。愛丁頓就一直在作這樣的努力。
電磁感應
由靜電的感應而生的靜電荷以及磁石對于軟鐵的類似作用,使早期實驗者想到利用伏特電池發出的電流也許可得同樣的效果。例如法拉第就用兩根絕緣線按螺旋的形式纏繞在同一根圓木筒上,但是,當他使強電流不斷地通過一根螺旋線時,他在另一螺旋線里的電流計上,沒有發現有什么偏轉。
他的第一個成功的實驗,在電學史上打開了一個新紀元。1831年11月24日,他向皇家學會這樣描寫這次實驗
把一根203呎長的銅絲纏在一個大木塊上,再把一根長203呎的同樣的鋼絲纏繞在前一線圈每轉的中間,兩線間用絕緣線隔開,不讓金屬有一點接触。一根螺旋線上連接有一個電流計,另一根螺旋線則連接在一套電池組上,這電池組有100對极版,每版四時見方,而且是用雙層銅版制造的,充分地充了電。當電路剛接通時,電流計上發生突然的极微小的效應;當電路忽斷的時候,也發生同樣的微弱效應。但當伏特電流不斷地通過一根螺旋線時,電流計上沒有什么表現,而在另一螺旋線上也沒有類似感應的效應,雖然整個螺旋線的發熱以及碳极上的放電,證明電池組的活動力是很大的。
用120對极版的電池組來重做這個實驗,也未發現有別的效應,但從這兩次實驗,我們查明了一個事實:當電路忽通時,電流計指針的微小偏轉常循一個方向;而當電路忽斷時,同樣的微小偏轉則循另一方向。
到現在為止,我用磁石所得的結果,使我相信通過一根導線的電池電流。實際上在另一導線上因感應而產生了同樣的電流,但它只出現于一瞬間。它更帶有普通來頓瓶的電震產生的電浪的性質,而不象從伏特電池組而來的電流;所以它能使一根鋼針磁化,而很難影響電流計。
這個預期的結果竟得到了證明。因為用纏繞在玻璃管上的中立的小螺旋線來代替電流計,又在這個螺旋線里安裝一根鋼針,再如前把感應線圈和電池組連結起來,在電路未斷以前將鋼針取出,我們發現它已經磁化了。
如先通了電,然后再把一根不曾磁化的鋼針安放在小螺旋線內,最后再把電路切斷,我們發現鋼針的磁化度表面上和以前一樣,但是它的兩极卻与以前相反。
用現今的靈敏電流計,我們很容易重做法拉第的實驗。只須用一個伏特電池作為原電流,而使原電路与副電路作相對的移動,或用一個永磁鐵和一個与電流計相聯的線圈作相對移動,都可以證明有同樣的暫時電流的發生。法拉第電磁感應的發現,為后來工業的大發展奠定了基礎。差不多一切實用上重要的電力机器,都是根据感應電流的原理制成的。
電磁力場
安培發現電磁定律,用數學公式把它表達出來以后,就感到滿足,沒有再去探索這种力靠什么机制傳播了。但承繼他的法拉第,不是數學家,對于中介空間或電磁力場的物理性質与狀態特別感到興趣。如果把一塊紙版放在磁捧之上,再拿一些鐵屑散布在紙版上,這些鐵屑將集合成許多線,表明磁力是沿這些線而起作用的。法拉第想象這樣的力線或力管將磁极或電荷連結起來,真的存在于磁場或電場之中,它們也許是极化了的質點所組成的鏈。如果它們象橡皮條那樣,處在緊張狀態之下,向縱的方向拉長,而向橫的方向壓縮,那么它們會在煤質中伸展出去,而將磁极或電荷向一起拉攏,這樣可以解釋吸引的現象。不論實際是否這樣,用法拉第的力線,來表示絕緣的媒質或電場中的應力与應變的現象,實在是一個便利的方法。
法拉第又從別的方面研究了電介質的問題。他發現在導体周圍的空气為虫膠或硫一類絕緣体所代替時,導体的靜電容量,即在一定電位或電壓下它能負荷的電量,便有增加;這個增加的比例他叫做那個絕緣体的電容率。
法拉第的見解超過了他的時代,而且他用來表達這些見解的術語,也不是當時所熟習的。三十年后,麥克斯韋將這些見解翻譯成數學的公式,并發展為電磁波的理論時,它們的重要性才被人認識(在英國立刻就被人認識,在其他國家比較慢)。這樣,法拉第就奠定了實用電學的三大部門,即電化學、電磁感應与電磁波的基礎。而且他堅決主張電磁力場具有极大重要性,這也是現代場物理學理論有關電的方面的歷史起點。
電磁單位
我們得感謝兩位德國的數學物理學家高斯(1777-1855年)与韋伯(W.E.Weber,1804-1891年),因為他們發明了一套科學的磁与電的單位。這种單位不是根据和它們同類的量任意制定的,而是根据長度、質量与時間三种基本單位而制定的。
1839年,高斯發表了他的《按照距离平方反比而吸引的力的一般理論》一書。電荷、磁极以及万有引力都适合這個關系。這樣,就可以給單位強度的電荷或磁极下這樣的定義:同相等的類似電荷或磁极在空气中相距一單位(1厘米),而以一單位的力(1達因)對該電荷或磁极加以排斥的電荷或磁极。如果用另一介質來代替空气,這個力就按一定的比例減少,他用k來代表電力,u代表磁力。k就是法拉第的電容率,在這里成為介質常數,u這個量后來叫做介質的磁導率。在這個基礎上高斯建立了一個宏偉的數學演繹的大廈。
安培与韋伯由實驗證明帶電流的線圈,与同大小同形式的磁鐵的作用相同,一個圓圈電流与一個在正交向上磁化的圓盤等效,所以一面是指北极,另一面是指南极的。這樣單位電流可定義為和單位磁力的磁盤等效的電流。根据這個定義,可以用數學方法導出如下結果:圓圈電流中心的磁場(即作用于單位磁极的力)等于2xc/r,這里c是電流的強度,r是圓圈的半徑,這個算式自然与由安培公式所導出的結果相合。所以只要將一顆小磁針懸挂在一大圓線圈的中心(這种裝置就是現今所說的正切電流計),再于電流通過線圈時,觀測磁針的偏轉,我們就可以以絕對單位或厘米一克-秒(C.G.S.)單位去測量電流。常用的電流單位(安培)按規定是上面所說的單位的十分之一,不過,多年以來為了實際應用与測量便利,一直是根据電解時析出銀的重量來做電流單位的標准,如上面所談到的。現在又有人提議重回到理論的定義上去。
熱与能量守恒
在十八世紀和十九世紀中,由于蒸汽机的發展,熱學成為一門具有非常重要的實際意義的科學,這反過來引起人們對于熱學理論的重新注意。
我們以前說過,按照熱質說,熱是一种不可秤量的流体。這個學說在啟發和解釋測量熱量的實驗方面起過有益的作用。但作為物理的解釋,分子激動說更合于敏銳的自然哲學家如波義耳和牛頓的口味。1738年,別爾努利(Daniel Bernouilli)指出,如果將气体想象為向四面八方運動的分子,那末這些分子對盛器的壁的沖擊,便可解釋气体的壓力,這壓力又必因气体被壓縮与溫度的增高而按比例增加,正如實驗所要求的那樣。
熱質論者解釋摩擦生熱的現象時,假定摩擦生出的屑末或摩擦后最終態的主要物質的比熱比摩擦以前的初態物質要小一些,因而熱是被逼出而表現于外的。但在1798年,美國人湯普遜(Benja-min Thompson后來在巴伐利亞成了朗福德伯爵Count Rumforo)用鑽炮膛的實驗證明發熱的量大致与所作的功的總量成正比,而与削片的量無關。可是熱的流体說仍然存在了半個世紀。
不過,到1840年,人們就開始了解自然界里各种能量至少有一些是可以互相變換的。1842年,邁爾(J.R.Mayer)主張由熱變功或由功變熱均有可能。邁爾在空气被壓縮的時候,所有的功都表現為熱的假定下,算出了熱的机械當量的數值。同年,英國裁判官兼科學家、以發明一种伏特電池著名的格羅夫(W.R.Grove)爵士,在一次講演中說明了自然間能量相互關系的觀念,并在1846年出版一本書《物理力的相互關系》中,闡述了這個觀念。這本書和1847年德國大生理學家、物理學家与數學家赫爾姆霍茨(H.L.F vonHelmholtz,1821-1894年)根据獨立的研究寫成的《論力的守恒》,是一般地論述現今所謂的“能量守恒”原理的最早著作。
1840至1850年間,焦耳(J.P.Joule,1818-1889年)以實驗方法測量了用電和机械功所生的熱量。他先證明電流通過導線所生的熱量,与導線的電阻和電流的強度的平方成正比例。他壓水通過窄管或壓縮一定量的空气或使輪翼轉動于液体中,而使液体生熱。他發現不管用什么方式作功,同量的功常得同量的熱,根据這個等值的原理,他斷定熱是能量的一种形式。雖是這樣,“經過多年之后,科學界領袖才開始贊同這种看法”,雖然斯托克斯告訴威廉·湯姆生(William Thomson):“他宁愿做焦耳的一個信徒”。1853年,赫爾姆霍茨訪問英國時就已經看見許多人對這個科學問題發生興趣,他到法國時又看見雷尼奧(Regnaull)已經采取了新的觀點。焦耳的最后結果表明:使一磅水在華氏55至60度之間溫度升高1度所需要消耗的功為772呎磅。后來實驗證明比較接近精确的數字是778呎磅。
焦耳用熱与功等价的明确的實驗結果,給予格羅夫所主張的“力的相互關系”、和赫爾姆霍茨所倡導的“力的守恒”的觀念以有力的支持。這個觀念就這樣發展成為物理學上以“能量守恒”得名的确定原理。能量作為一個确切的物理量,在那時的科學上還是新東西。這個名詞所表示的觀念,曾經用不准确的、具有雙重意義的“力”一詞來表達。托馬斯·楊指出,這樣就把“能量”和“力”混淆起來了。能量可以定義為“作功的力”,而且如果兩者的轉換是完全的,能量便可以用所作的功來測度。“能量”一詞用于這种專門的意義應歸功于蘭金(Rankine)与湯姆生。湯姆生采用了托馬斯·楊所提出的把力和能量區別開來的主張。
焦耳的實驗證明在他所研究過的情況里,一個体系中能的總量是守恒的,功所耗失之量,即作為熱而出現。一般的證据引導我們把這個結果推廣到其他的變化上去,例如机械能變為電能,或化學能變為動物熱之類。直到近年為止,一切已知的事實都适合于這句話:在一個孤立的体系中,總的能量是守恒的。
這樣确立的能量守恒原理可以和較早的質量守恒原理相媲美。牛頓的動力學的基礎就在于這樣一种認識:有一個量,--為了便利起見,稱為一個物体的質量——經過一切運動而不變。在化學家手里,天秤證明:這個原理在化學變化中也一樣地有效。在空气中燃燒的物体,它的質量并不消失。如果把所產生的物質收集起來,它們的總量必等于原物体与所耗的空气的份量的總和。
能量也是這樣的:質量以外的另一個量出現在我們的意識里,主要是因為它經過一系列的轉換仍然不變。我們覺得承認這個量的存在,把它當作一個科學的概念,并且給它起一個名字,是有种种便利的。我們稱它為能或能量,用所作的動量或發生的熱量來測量它的變化,并且費了許多工夫,經過許多疑惑,才發現它的守恒性。
十九世紀的物理學,沒有一個方法可以創造或毀滅質与能。二十世紀出現了一些跡象,說明質本身就是能的一种形式,從質的形式轉變為能的形式并非不可能的事,但直到近些年為止,質与能是截然不同的。
能量守恒的原則,約在1853年為湯姆森(Julius Thomsen)首先應用于化學。他認識到在化學反應里所發出的熱是這個系統的合能量在反應前后的差异的衡量尺度。既然在一個閉合的系統中,最后的能量和最初的能量必然是相同的,因此,在某些情況下,我們就有可能預言這個系統的最后狀態,而不必顧及中間的步驟,也就是一步跳到一個物理問題的解答,而不必探究達到目標的過程,象惠更斯對于某些比較有限的力學問題所做過的那樣。由于這個實際的用途和它固有的意義,能量守恒原理可以看做是人類心靈的重大成就之一。
但是它有自己的哲學上的危險性。由于質量守恒原理和能量守恒原理在當時可以研究的一切情況下無不有效,這兩個原理就很容易被引伸為普遍的定律。質量成了永恒而不滅的;宇宙里的能量,在一切情形下及一切時間內都成了守恒而不變的。這些原理不再是引導人們在知識領域內憑借經驗逐漸前進的万無一失的響導,而成了有效性可疑的重要哲學教條了。
气体運動說
1845年,瓦特斯頓(J.J.Waterston)在一篇手稿備忘錄中,進一步發展了由于熱与能統一起來而顯得更加重要的气体運動說。這篇備忘錄在皇家學會的檔案擱置多年而被人遺忘了。1848年,焦耳也研究了這個問題。這兩位科學家把這個理論推進到別爾努利所沒有達到的地步,并且各不相謀地算出分子運動的平均速度。1857年,克勞胥斯(Clausius)才首先發表了正确的物質運動說。
由于分子碰憧的机會很多,而這种碰撞又假定帶有完全的彈性,所以在任何瞬間,所有的分子必定向一切方向,帶著一切速度而運動。全部分子的平動總能量可以量廢气体的總熱量,而每一分子的平均能量可以量廢溫度。從這些前提,我們可以用數學方法推導出气体的壓力P等于1/3nmV2,這里n是單位容積中的分子數,m是每個分子的質量,V2是气体速度平方的平均值。
但nm是單位容積中气体的總質量,即是它的密度,所以如果溫度和V2不變,則气体的壓力与其密度成正比例,或与其容積成反比例,這是波義耳由實驗發現的定律。如果溫度變化的話,由于p与V2成比例,壓力必隨溫度而增加,這就是查理定律。如果我們有兩种气体在同壓与同溫之下,從以上為方程式可知在單位容積中兩气体的分子數相等,這是阿伏伽德羅從化學事實得到的定律。最后,就這兩种气体來說,分子的速度V必定与密度nm的平方根成反比例,這關系可以解釋气体滲透多孔間壁的速度,這正是1830年格雷厄姆(Thomas Graham)由實驗所發現的定律。
從這些演繹可見別爾努利、焦耳和克勞胥斯等提出的初步的气体運動論和气体的比較簡單的實驗性質是符合的。而且如瓦特斯頓和焦耳所表明的,這個學說使我們可以近似地算出分子的速度。例如,在攝氏零度及水銀柱760毫米標准大气壓,或每平方厘米1.013×106達因的壓力下,氫的單位質量的容積是11.16升或11.160立方厘米。因此從P=1/3nmV2方程式得到V為每秒1844米,或每秒一英里多。氧元素的相應數字是每秒461米。這些數字是V2的平均值的平方根;V本身的平均值,即分子速度.稍小一些。1865年,勞施米特(Loschmidt)根据气体運動論,首先算出一立方厘米的气体在0”C和大气壓下所有的分子數目為2.7×1019。
麥克斯韋与波爾茨曼(Boltzmann)將高斯由概率理論所導出的誤差律應用到速度分配的問題上去,這個理論現時對許多研究部門都十分重要。它表明由于分子的偶然碰撞的机會极多,它們可分為几群,每一群在某一速度范圍內運動,其分布如圖5所示。橫標代表速度,縱標代表以某一速度運動的分子數。如果以最可能的速度為單位,我們就可以看出,速度三倍于最可能速度的分子數差不多可以略而不計。人們還可以划出類似的曲線來表示靶上槍彈分布,物理量度中的誤差分布,按身長、体重、壽命長短、或考試中表現出的能力等划分的人群的分布。不論在物理學、生物學或社會科學上,概率理論与誤差曲線都有很大的重要性。預測一個人的壽命長短或一個分子在未來某時刻的速度,是不可能的;但如果有了足夠數目的分子或人,我們就可用統計的方法來加以處理,我們可以在极窄狹的范圍內,預測有好多分子在某一速度范圍內運動,或好多人將死于某年。從哲學上來說,我們不妨說我們已經達到一种統計決定論,雖然在這個階段里,個体的不确定仍然存在。
波爾茨曼与沃森(Watson)查明.原來以他种速度運動的分子有歸于麥克斯韋-波爾茨曼分布的傾向;因為這是最可能的分布。他們證明這种傾向与熱力學上一個名為“熵”的量趨于最大值的傾向相當。達到這种最可能的情況——即熵達于最大值,速度按誤差定律分布的過程,和洗紙牌相似。這种現象在自然界里是隨時間的推移自然出現的;現時在科學上和哲學上,都有极大重要性。
麥克斯韋還指出气体的粘滯度必依其平均自由程而定,所謂平均自由程即一分子在兩次碰撞之間所經過的平均路程。氫的平均自由程約為17×10[-6]厘米,氧為8.7×10[-6]厘米。碰撞的頻率約為每秒10[9]次,這個數字很大,說明為什么雖然分子的速度很大,气体的彌散仍然很慢。气体的粘滯度并不象一般人所想象的那樣隨密度而變小,而是隨著气体的被抽出,始終保持不變,除非密度達到很低的水平。這些理論的結果為實驗所證明,因此這個理論的比較高深的部分很早就得到人們的信任。
根据气体運動論,溫度是用分子的平動的平均能量來度量的,但這些分子也可能具有由轉動、振動等而來的能量。麥克斯韋和波爾茨曼表明總能量應与分子的“自由度的數目”,即決定一個分子的位置所需要的坐標數成比例。空間一點的位置決定于三個坐標,因此決定溫度的分子整体的運動,含有三個自由度。設自由度的總數為n,當气体受熱時,熱能的一部分3/n變為平動的能量,以使溫度增高,其余(n-3)/n則被分子用到其他運動上去。气体在容積守恒的情況下加熱時,所有的熱都用來增加分子的能量,但如壓力不變,容積必增加,因此它必反抗大气的壓力而作工。我們可以證明,從這里可以提出如下結論,在定壓和定積的情況下,兩种比熱之比y可以表為1+2/n。所以,如n=3,Y=1+2/3=1.67。在麥克斯韋進行這個計算的時候他還不知道有什么气体有這樣的比值,但后來發現分子各單原子的气体,如汞蒸气、氬和氦都合于這個計算結果,因此,就熱能的吸收而論,它們与簡單的質點并無分別。平常的气体如氫与氧是雙原子的分子。它們的γ等于1.4,表明這些分子有五個自由度。
如果將溫度的改變一并加以考慮,波義耳定律--pv=常數——可擴張為pv=RT,P是一個常數。分子間的吸引按密度的平方a/v2而變化,這里a是一個常數,所以,其效果將p增加到P+a/v2。分子本身所占的容積,不能再加壓縮,所以其效果將v縮減到v-b。因此,范·德·瓦爾斯(Van der Waals)于1873年得到以下的方程式:
(p+a/v2)(v-b)=RT
這個方程式用來表達某些“非理想气体”,同波義耳定律有出入的情況,頗為合适。
有几位物理學家,特別是安德魯斯(Andrews),用實驗方法對這种气体加以考察。安德魯斯在1859年左右對气体与液体兩种狀態的連續性進行了研究。他指出每种气体都有其确定的臨界溫度,在這溫度之上,無論壓力怎樣大,都不能使這种气体液化。因而气体液化的問題是一個怎樣把溫度降低到臨界點以下的問題。
植物學家布朗(Robert Brown)1827年在顯微鏡下看見极微質點的不規則運動,從而直接證明了分子的運動;1879年拉姆賽(William Ramsay)在解釋這個現象時,認為這是由于液体分子沖擊懸于液体中的質點而造成的。克魯克斯(Crookes)注意到如將輕的風車翼一面涂黑,裝置在高度真空管中的旋轉軸上,再把它放在日光中,它必按光亮的一面的方向旋轉。麥克斯韋在解釋這种旋轉時認為這是由于黑的一面吸收了較多的熱而造成的。分子受熱激動,以較高的速度跳躍,碰撞風車翼時,便將黑面向后推動。
熱力學
1824年,“胜利的組織者”的儿子卡諾(SadiCarnot),指出每一熱机(或熱引擎)必須有一熱体或熱源与一冷体或冷凝器,當机器工作時,熱即由較熱的物体傳到較冷的物体。卡諾在其手稿中談到能量不滅的觀念,但有很長時間,人們都按照熱質說去了解他的研究成果,以為熱經過机器后在量上不減,是靠溫度的降低來作工的,正象水田高處降落,使水車工作一般。
卡諾認為要研究熱机的定律,必須首先想象最簡單的情形;熱机全無摩擦,熱不會因傳導而散失。他還認識到在研究机器的工作時,我們必須假定熱机通過一個完全的觀察的循環,作工的物質,無論是蒸汽也好壓縮空气也好或其他任何東西也好,經過工作之后仍然回复到原來狀態。如果不是這樣,机器可能從工作物質內部的能量中吸取動或熱,全部的功可能就不全是經過机器的外部的熱所做的了。
卡諾的循環說的現代形式是克勞胥斯与維廉·湯姆生(即后來的凱爾文男爵)完成的。當功變成熱或熱變成功的時候,其間的關系可以用焦耳的結果來表示。不過雖然永遠有可能把一定量的功全部變成熱,反過來要把一定量的熱全部變成功,一般來說卻是不可能的。在蒸汽机或其他熱机里,所供應的熱量只有一小部分變成机械能,其余的部分由机器中較熱部分傳到較冷部分,不能做有用的功。經驗證明:熱机開動時從熱源取來一定量的熱H,而把其中的一部分熱量h傳給冷凝器。這兩個熱量之差(H-h)就是可變為功W的最大熱量,而實際完成的功与所吸收的熱量之比W/H,可作為這個机器的效率E。
一個理論上完善的机器,既不會由傳導失去熱,也不會由摩擦失去功,所以
W=H-h,
而E=W/H=[H-h]/H。
一切完善的机器具有相同的效率,否則,我們便可把兩個机器連給在一起,從冷凝器的熱能中得到功,或通過一种自動的机制,繼續不斷地把從冷体吸到熱体中去,這兩者都是同經驗不合的。因此,效率以及由熱体吸取的熱与冷体放出的熱之比,是与机器的形式或工作物質的性質無關的。和這些數量有關的只有熱源的溫度T和冷凝器的溫度t;而吸收的熱与放出的熱之比,只要寫成了T/t=H/h;的形式時,便可用來做兩個溫度之比的定義,于是:
E=(H-h)/H=(T-t)/T。
這樣,湯姆生就制定出一种熱力學的溫標。它是絕對的,因為它与机器的形式或工作物質的性質無關。如果一個完善机器的冷凝器的溫度是零度,即t=0,或E=1,那就是說所有吸收都轉變為功,沒有熱到冷凝器去,這時效率是1。任何机器不能作比它吸收的熱當量更多的功,或者說任何机器的效率都不能大于1。因此這种溫標的零度是絕對零度,即沒有比這更冷的溫度了。
這樣規定的熱力學的溫標,純粹是理論上的。實際上,我們根本無法測量一個完善机器所吸收的熱量与所放出的熱量之比,來比較這兩個溫度。單說一個理由:我們根本無法制造出一個完善的机器。因此我們必須把熱力學的溫標變成實用的東西。
焦耳在一個研究里,和他以前的邁爾一樣,利用對空气進行壓縮的辦法來把功變為熱。不過為了說明他采用這個辦法的理由,焦耳重新進行了蓋伊-呂薩克的被忘記了的實驗,并且證明讓空气膨脹而不作工,則溫度沒有可覺察的改變。由此可見當气体膨脹或收縮的時候,气体的分子狀態沒有什么變化,在壓縮空气時,所作的功都變形為熱。湯姆生与焦耳設計了一個更精細的實驗方法,證明將气体壓過一個多孔的基,然后任其自由膨脹,溫度的改變實在有限,空气稍為變冷,氫气甚至稍稍變熱。根据數學上的考慮可以知道,如果用空气或氫气制成溫度計(零度接近-273℃),這种溫度計差不多和絕對的或熱力學的溫標相合,其間的小小差异,可以從自由膨脹的熱效果計算出來。
熱力學上的推理所得出的推論,不但使工程師可以把熱机理論放在堅實的基礎之上,而且在許多別的方面大大推動了現代物理學和化學的進步。法拉第單單利用壓力,就在一個簡單儀器中將氯气液化了。但絕對溫標的理論以及湯姆生和焦耳的多孔塞實驗為現代的一系列研究開辟了道路。經過這一系列研究,終于使一切已如气体都液化,并且最后證明各种類型的物質都在三种狀態下連續存在。多孔塞的效果在平常溫度下固然很小,在把气体先行冷卻以后,就變得很大。如果不斷迫使一种冷气体通過一條管嘴,它會變得更冷,并且可以用來冷卻后面流來的气体。這樣,這個過程的效果就累積起來,气体最后就被冷卻到臨界溫度而液化。杜瓦(James Dewar)爵士在1898年用這方法使氫液化,卡麥林-翁內斯(Kamerlingh-Onnes)在1908年把最后剩下來的氦气液化。杜瓦用來進行液化實驗的真空玻璃瓶,就是現今人所熟習的溫水瓶。
有不少人研究過這种极低溫對于物体性質的效應。最顯著的一种變化便是電的傳導率的急劇增大;例如鉛在液態氦的溫度(-268.9℃)的導電率比在0℃時,約大十億(109)倍。電流在這种低溫的金屬電路里,一經開始,使經歷許多小時而不稍減。
要從熱的供應得到有用的功,溫差是必需的。但在自然界中,通過熱的傳導与其他方式,溫差是不斷變小的。因此在一個有不可逆的改變進行的孤立的系統中,可作有用的功的熱能傾向于不斷地變得愈來愈少,反之,克勞胥斯稱為熵的數學函數(在可逆的系統中是常數),卻傾向于增加。當可用的能達到最小限度或熵達到最大限度的時候,就再沒有功可做了,這樣就可以确定這個系統的平衡所必需的條件。同樣,在一個等溫(即溫度不變)的系統中,當吉布斯(Willard Gibbs)所創立的另外一個數學函數:“熱力學的位勢”到了最小限度的時候,也可以達到平衡。這樣,克勞胥斯、凱爾艾、赫爾姆霍茨、吉布斯与奈恩斯特(Nernst)等就創立了化學和物理學平衡的理論。現代的物理化學的很大一部分,以及許多工業上重要的技術應用都不過是吉布斯熱力學方程式的一系列的實驗例證而已。
最有用的結果之一就是所謂的相律。設想一系統里有n個不同的成分(例如水与鹽兩個成分)和r個相(例如兩個團体、一個飽和溶液和一個蒸汽等四個相),根据吉布斯定理,自由度的數目F將是n-r,這上面還須加上溫度与壓力兩個自由度。因此相律可表為下式:
f=n-r+2
以前發現的第二個方程式給出如下四個量——即任何物態變化的潛熱L,絕對溫度T,壓力p与容積的變化u2-u1——之間的關系,即
L=T(dp/dT)(v2-v1)或dp/dT=L/T(v2-v1)。
這個方程式的原理本來是詹姆斯·湯姆生(James Thomson)所創立的,1850年左右,由凱爾文男爵、蘭金和克勞胥斯等人加以發展,以后再由勒·夏特利埃(Le Chatelier)應用到化學問題上。潛熱方程与相律方程合在一起提供了不同的相的平衡的一般理論,以及系統不平衡時壓力隨溫度的變化率。由此也可以知道,外界對系統的作用在系統內造成一种對抗的反作用。
在相律方程里,如r=n+2,則F=0,這個系統便是“非變系”。例如,在只有一個成分的情況下,當水質的冰、木和汽三相集在一起的時候,它們只有在某一特殊溫度才能達到平衡,而且只有在壓力調整到某一特殊數值的時候,才能達到平衡。如果只有兩相,例如水与汽,則r=n+1与F=n=1,因而系統只有一個自由度。在PT曲線上任何一點上,這兩相都可以達到平衡,這曲線上每點的斜率都可由潛熱方程測定。不只一個成分的系統自然更加复雜。
相律關系在科學与工業上极重要的一种應用,便是合金結构的研究。這一研究為人們提供了具有特殊性質、适合于特殊用途的許多金屬。這方面的理論主要是利用三种實驗方法創立起來的:(1)以适當的液体侵蝕金屬,放在顯微鏡下研究其磨光的截面;在1863年,英國謝菲爾德(Sheffield)的索爾比(H C.Sorby)和德國夏羅騰堡(Charlottenburg)的馬頓斯(Martens)創立了這种方法,主要是用來研究鐵,其后,這個方法又有很大的改進。這個方法清楚地揭示了金屬与合金的晶体結构。(2)熱方法。讓熔融的金屬冷卻,對時間和溫度加以測量。當物態改變,例如由液態變成固態時,溫度的降落變經,或有一段時間完全停頓。在這方面,可以舉出魯茲布姆(Roozeboom)關于吉布斯理論的研究(1900年)和海科克(Heycock)与內維爾(Neville)的實驗為例。(3)X射線方法。這個方法是勞厄(Laue)与布拉格爵士父子創立的,它揭示了固体(不論其為鹽類、金屬或合金)的原子結构,并開辟了一般原子研究的新領域。
雙金系的最簡單的平衡可以用海科克和內維爾關于銀与銅的研究為例來說明。純銀沿曲線AE(圖6)從液態里凝凍,純銅沿曲線BE從液態里凝凍。在交點E,銀、銅兩晶体同時出現,因而凝固是在不變的溫度下進行的。在這种合金里,銀占40%,銅占60%,其結构是有規則的,因而名叫“易熔合金”。
如果固体象液体一樣可以改變其組成成分,我們將得著“和晶”或“固溶体”,与更复雜得多的現象。魯茲布姆首先用吉布斯的理論,闡明了這些現象。在表示固溶体的圖里,固体的溶度曲線的交點指明了一個极低的、以易熔點得名的溫度。在這里,兩個固態相一塊從其他固態相結晶出來,而形成一种在結构上類似易熔合金的易熔質。圖7是說明鐵碳(碳少于6%)混合物的魯茲布姆圖的現代形式。這個圖可以說明現已查明并且有了名稱的各种化合物与固溶体,甚至說明了完全是固体的各种合金在确定的溫度下的變化。這种金相圖幫助我們探索組成成分、溫度調節与物理性質之間的關系,以及鐵和鋼“回火”的結果。
近年來制出了許多具有各种特殊性質、适合各种用途的新合金,特別是鐵的合金。供和平目的使用的合金如不銹鋼,供制造武器使用的鐵合金,都含有少量的鎳、鉻、錳、鎢等金屬。這些金屬經過适當的熱處理之后,可使鐵的剛硬度或堅韌度增大或具有其他需要的性質。這些近年來的發展都是建立在上述理論与實驗的基礎之上的。以下舉出几個這樣的合金的例子:
將3%的鎳加在鍋內,增加強度而不減少延世。如果使用36%的鎳的話,由于碳含量低,膨脹系數將變得很微小,這种合金可用于很多用途,稱為“殷鋼”或“因瓦(invar)合金”。銘能使碳化物穩定,加少許于鋼內,所造成的合金能抗腐蝕。鎳鉻鋼在机器制造上很重要,特別是含有少許鉬的鎳鉻鋼。錳也能使碳化物更加穩定,如果錳的成分很多則造成的合金易脆,錳的成分再多一些,最后就制成含碳12%的“高錳鋼”。對這种合金的表面加工,可使其堅硬,獲得极高的抗磨性,常用以制造碎石机的部件。鎢原子量大,能減少固游体里的移動性,因而保持高度的抗蠕變能力,并延緩相變。鎢鋼与鈷鋼相同均可用以制造恒磁体。
在非鐵合金里,鋁的合金特別有趣,也特別有實用价值。1909年左右,維耳姆(Wilm)等人開始對于這种合金進行認真的研究。后來主要是由于航空工業需要質輕而強的金屬,這一研究又有進一步的發展。鋁合金里有一种名叫“硬鋁”,含銅4%,鎂0.5%和錳O.5%,其余95%為鋁。為時間所硬化后,硬鋁的強度可与軟鋼相比。還有許多別的鋁合金与其他金屬的合金,各具有特殊的性質。
熱力學第一定律是能量守恒原理,第二定律是可用的能量愈來愈少。在把這些觀念擴大應用到整個恒星宇宙上的時候,就有人認為,宇宙間的能量不斷地通過摩擦轉化為熱而浪費了,同時,可用的熱能又因溫差減少而不斷地減少起來。于是有些物理學家便想到在遙遠的將來宇宙中所儲蓄的一切可用的能量可能都要轉化成熱,平均分布到保持机械平衡的物質中,以后就永遠不可能再有任何變化了。但這個結論建立在几個未經證明的假設上。(1)它假定根据有限的觀察結果得出的結論,在大体上還沒有弄清的更廣泛的局面中同樣有效;(2)它假定恒星宇宙是孤立的体系,沒有能量可以進去;(3)它假定單個分子由于互相碰撞,速度不斷地改變,我們不能追蹤它們,把它們分為快速与慢速兩類。
麥克斯韋想象有一個极小的生物或妖魔,有极微妙的感覺,可以跟蹤每個分子的行動,負責管理牆壁上一扇無摩擦的滑動門,牆壁兩邊有兩個裝滿气体的房間。當快速分子由左到右運動時,小妖立刻開門,當慢速分子來時,他立刻關門。于是快速分子聚集在右室,慢速分子聚集在左室。右室里的气体逐漸變熱,左室里的气体逐漸變冷。這樣,有了控制單個分子的能力就可以使彌散的能量重新集中起來。
在十九世紀所了解的自然界的情況下,在我們只能用統計的方法來處理分子的時候,能量耗散的原理原是不錯的。人們生活与活動需要的能量的供應量好象不斷地愈來愈少,而熱力學上的衰變的過程也有慢慢消滅宇宙里的生命的危險。按照新近的知識,這個結論究竟在多大程度上得到修改或證實,我們將在后面的一章內再加論述。在這里,我們應該指出,當分子的速度按照麥克斯韋-波爾茨曼定律分配的時候,熵達到最大值——即能量的耗散達到最大限度——的熱力學條件就達到了,而這种分配的概率卻是一個最大值。這樣,就把熱力學同概率論的已知定律及物質運動論聯系起來了。
光譜分析
那种把天和地區別開來的傳統看法,經過整個中世紀,人們還是這樣相信,但伽利略与牛頓卻把這种看法打破了。他們用數學方法与觀察方法證明,通過實驗确立的落体定律在整個太陽系中一樣适用。
可是要最后證明天地同一,不但需要天地在運動方面是類似的,而且還需要證明天地在結构上与組成成分上也是類似的,還需要證明构成地上物体的習見化學元素,在太陽、行星与恒星的物質中也一樣的存在。這好象是一個無法解決的問題。可是在十九世紀中葉卻找到了一個解決的辦法。
牛頓已經證明日光通過棱鏡所形成的彩色光帶,是由于白光分析成物理上比較簡單的成分的緣故。1802年沃拉斯頓發現太陽的光譜被許多暗線所截斷;1814年弗朗霍費(Joseph Fraunhofer)重新發現這些暗線,并用多個棱鏡增加光譜的色散度,仔細地將暗線的位置描繪下來。另一方面,1752年,梅爾維爾(Melvil)首先觀察到,金屬或鹽類的火焰所造成的光譜,在黑暗的背景上呈現特殊的彩色明線;1823年,約翰·赫舍爾(John Herschel)爵士又一次表示這些譜線可以用來檢驗金屬的存在。這建議引起人們對于譜線位置進行觀測,并加以描繪与記錄。
1849年,弗科研究了炭极間的電弧光所生的光譜,發現在黃橙兩色之間,有兩條明線,恰在弗朗霍費稱為D的兩條暗線位置上。弗科更發現當日光通過電弧時,D線便比較平常為暗,若將一個炭极的光(它本身產生連續光譜而無暗線)通過電弧,則D線又會出現。弗科說:“可見,電弧光本身是發生D線的,但若D線從旁的光源而來,電弧光就加以吸收。”
弗朗霍費譜線的理論好象首先是由斯托克斯(George GabrielStokes,1819-1903年)在劍橋的講演中加以闡明的,可是由于他特有的謙遜,他并沒有將他的見解廣泛宣傳。任何机械体系都能吸收与自己的天然振動合拍的外來能量,正象只要對儿童秋千不斷地給予和它的自然擺動周期一致的一系列小沖擊,便能使它動蕩不停一樣。太陽外圍的蒸气分子也必定能吸收從比較熱的內部射出的特殊光線的能量,只要這些光線的振動周期同蒸气分子的振動周期一致。這樣射來的光必定缺少了具有那种特殊振動周期的光(即某一色彩),結果太陽光譜中便產生一條暗線。
1855年,美國人奧爾特(David Alter)描述了氫和其他气体的光譜。1855至1863年間,本生(von Bunsen)在羅斯科(Roscoe)的合作下,進行了一系列的實驗來研究光的化學作用,1859年,他与基爾霍夫(Kirchhoff)合作創立了最早的光譜分析的精确方法,于是化學元素,盡管只有微量,也可由它們的光譜檢查出來。銫与銣兩個新元素就是用這個方法發現的。
本生与基爾霍夫在事先不知道弗科實驗的情況下,讓發連續光譜的白熱石灰光,通過含有食鹽的酒精火焰,結果,看到了弗朗霍費的D譜線。他們又把鋰放在本生煤气燈中重新進行了這個實驗,找到一條在太陽光譜中找不到的暗線。他們斷定太陽的大气中有納,但沒有鋰,或者是含量太少,觀察不到。
這樣開始的天体光譜學,經過哈金斯(Huggins)、詹森(Jan-ssen)与洛克耶(Lockyer)等人的努力,有了很大的發展。1878年,洛克耶在太陽色球層的光譜的綠色部分看見一條暗線,和地上光譜中任何已知線都不符合。他和弗蘭克蘭(Frankland)共同預言,太陽里有一個可以說明這种現象的元素;他們并把這個元素命名為氦。1895年,拉姆賽在一种結晶鈾曠里發現了這個元素。
1842年,多普勒(Doppler)指出,當一個波源与觀測者作相對運動時,所觀測到的波的頻率便會發生改變。如果波源向觀察者逼近時,每秒鐘達到觀察者的波數必定增多,結果是聲或光的頻率變高。反之,波源离觀察者而去時,聲或光的頻率降低。在快車穿過車站時,汽笛聲音由高而低,就充分說明了這种變化。如果一顆星向地球而來,其光譜線必向紫色一端移動,如果离地球而去,則向紅色一端移動。這种多普勒效應雖然很小,卻可以量度,經過哈金斯及以后許多人研究,使我們對恒星運動增長了不少知識,在近來還使我們對其他現象增長了不少知識。
同時光与輻射熱具有相同的物理性質,也得到充分證明。1800年,威廉·赫舍爾(William Herschel)爵士指出,將溫度計放在太陽光譜中就可以看出,在可見的紅色光之外,仍有熱效應。過后不久,利特爾(Ritter)發現可見的紫色光以外仍有射線,可使硝酸銀變黑。1777年,舍勒(Scheele)就發現了這种攝影作用。1830至1840年間,梅洛尼(Melloni)證明看不見的輻射熱和光一樣,有反射、折射偏振、干涉等性質。有許多物理學家,特別是基爾霍夫、丁鐸爾(Tyndall)与鮑爾弗·斯特沃特(Balfour Stewart)把發射与吸收兩种強度的等价原理,擴大應用到熱輻射。他們發現,一個能吸收一切輻射的黑体,受熱時也能發射一切波長的輻射。普雷沃斯特(Prevost)在其交換理論(1792年)中指出,一切物体都輻射熱量,只是在平衡時,其所吸收之量恰等于所發射之量。
麥克斯韋從理論上證明輻射對它所照射的面施加一种壓力,這壓力雖然极其微小,但近年來已用實驗方法加以證實。1875年,巴托利(Bartoli)指出這种壓力的存在使我們想象一個充滿輻射的空間,可以有理論上的熱机的汽缸作用。1884年,波爾茨曼證明黑体的總輻射按其絕對溫度的四乘方而增加,或H=aT4。斯蒂芬(Stefan)在1879年就已經憑經驗發現了這個定律。這個結果很有用,不但對于輻射理論很有用,而且可以利用這個結果,通過觀察所放出的熱能來測量火爐的溫度,甚至太陽和恒星的表面溫度。溫度增加時,不但總輻射照這個方式增加,而且所發射能量的最大值,也向比較短的波長的方向移動。
最后,一個元素的不同譜線的頻率之間的确定關系,雖然到二十世紀才在物理學上顯出無比的重要,在十九世紀時就已開始引起人們的注意。1885年,巴爾默(Balmer)指出氫元素的可見光譜里的四條線,可用一個經驗公式來代表。后來哈金斯指出,這個公式還可表達紫外譜線的頻率以及星云譜線和全食時日冕光譜線的頻率,因此,這些可能都是氫元素的譜線。由此,他斷定星云和日冕之內有氫元素存在。
電波
上面說過,法拉第的許多電學實驗工作應歸功于他對電介質或絕緣質的重要性的本能的理解。當電流的作用越過空間使磁針偏轉或在不相聯的另一電路上產生感應電流時,我們要么就必須想象有一种未經解釋的“超距作用”,要么就必須想象空間里有一种傳達效應的橋梁。法拉第采納了第二种想法。他假想在“電介极化”里有一些力線或一些質點鏈。他甚至想象它們离開來源后,可以在空間里自由行進。
麥克斯韋(1831-1879年)把法拉第的想法寫成數學公式。他指出法拉第電介极化的改變即相當于電流。既然電流產生磁場,磁力与電流正交,而且磁場的改變又產生電動力,顯然磁力与電力有相互的關系。因此,當電介极化的改變在絕緣介質中,四面傳布時,它必作為電磁波而行進,電力与磁力則在前進的波陣面上相互正交。
麥克斯韋所發現的微分方程式說明,這种波的速度只隨介質的電与磁的性質而不同(這也是很自然的),而這個速度可表為
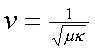
式內μ代表介質的磁導率,κ代表介電常數或電容率。
由于兩個電荷間的力与k成反比,兩個磁极間的力与μ成反比,所以用這兩种力來規定的電与磁的單位必含k与μ。而任何單位的靜電值与電磁值之比,例如電量的單位,必含μ与k的乘積。所以只要通過實驗比較兩個這樣的單位,便可測定電磁波的速度v的數值。
麥克斯韋和几位物理學家發現,這樣測定的v的數值為每秒3×1010
厘米,和光的速度相同。于是麥克斯韋斷定光是電磁現象,有了一种以太就可以傳播光波和電磁波,無需再臆造好几种以太了。原來光波与電磁波,波長雖然不同而卻是同類的。
但是我們怎樣對待人們化費了那么多心血來研究的彈性固体以太呢?我們究竟應該把電磁波看作是“准固体”里的机械波呢還是應該按意義還不明白的電与磁來解釋光呢?麥克斯韋的發現,第一次向世人提出了這個難題。可是他卻加強了人們對于傳光以太存在的信心。很明顯,以太既能傳光,也能執行電的作用。
麥克斯韋的研究成果在英國立刻得到承認,但在大陸上則沒有得到應得的注意。到1887年,赫茲(Heinrich Hertz)才用感應圈上的電花所發生的振蕩電流,在空間產生并檢驗到電波,而且用實驗方法證明電波具有許多与光波相同的性質。如果真的有以太,它里面就擠滿了“無線電波”,而這些波絕不是在空气里傳播的。這一發現主要應該歸功于麥克斯韋与赫茲的工作。
麥克斯韋要求物理學家集中注意絕緣的介質,以為這是帶電系統中最重要的部分。很明顯,電流的能量是在介質中通過的,而電流自己不過是這种能量耗散為熱的路線,這條路線的主要功用是引導能量沿著有可能耗散的路徑前進。在很迅速變化的交流電中,如在感應圈的電花的電流或閃電電花的電流中,能量剛進入導体,電流方向就改變了。因此,只有導線或避雷針的表皮可以有效地帶電,電阻也就比在穩恒電流的情況下高得多。
麥克斯韋理論的主要困難是不能對電荷給予明白的說明,至少不能對法拉第的電解實驗所指明的相异的原子電荷給予明白的說明。麥克斯韋死后不久,原子電荷的觀念就成了极重要的問題,我們現在就必須加以論述。但是我們須得先离開本題,去作一點題外的敘述。
化學作用
很早以來,化學作用的原因与机制便成為臆度的題材,引起牛頓很多的注意。1777年,溫策爾(C.F Wenzel)進行了确定的測量,想通過觀察化學變化的速度來估計酸類對于金屬的化學親合力。他發現化學反應的變化率与酸類的濃度,即試劑的有效質量成比例,貝爾托萊(Berthollet)也獨立得到這個結果。
1850年,威廉米(Wilbelmy)研究了蔗糖加酸時的“反旋”,即蔗糖分子分解成為較簡單的左旋糖和右旋糖的過程。他發現當蔗糖液的濃度在反應進行過程中減少的時候,變化率便与時間的几何級數成比例而減少。這就是說在任何瞬間离解的分子數与當時存在的分子數成比例——假定蔗糖分子的离解互不相干,這种結果是很自然的。不管什么時候,只要這個關系對于某一化學變化有效,我們便可推斷分子是單個地在起作用,而這种變化便稱為單分子反應。
另一方面,如果兩個分子互相起作用(雙分子反應),變化率顯然決定于分子碰撞的頻率,而這頻率又与兩种起作用的分子的濃度或有效質量的乘積成比例。如果分子的濃度相等,則此乘積將等于濃度的平方。
如果反應是可逆的,當兩种化合物AB与CD互相作用而成AD与CB時,后二种同時也互相作用,而回到AB与CD;當相反的變化以同等變化率進行時,即當AB+CD←→AD+CB時,必成平衡狀態。
這种動態平衡的觀念是威廉森(A.W.Williamson)在1850年首先明白提出的。1864年,古德貝格(Guldberg)与瓦格(Waage)對化學作用的質量定律加以完滿的表述;杰利特(Jellet)在1873年,范特-霍夫(Van’t Hoff)在1877年又重新發現了這個定律。這個定律不但如上所述,可由分子運動理論推出,也可根据熱力學原理從淡液体系的能量關系誘導出來。它在許多化學反應中得到實驗上的證明。
上面說過,蔗糖的反旋在有酸類在場時進行得很快,否則進行得极慢。酸類并沒什么變化,它好象只促進反應,自己并不參加反應。這一現象在1812年首先為基爾霍夫發現。他發現在淡硫酸溶液中,淀粉可變化為葡萄糖。戴維注意到鉑能使醇蒸汽在空气中氧化。多貝賴納(Dobereiner)更發現鉑的粉末可使氫氧二气化合。1838年,德拉托爾(Cagniard de Latour)与施旺(Schwann)各不相謀地發現糖所以能發酵而成酒精与二氧化碳,是由于一种微生物的作用,柏采留斯更指出發酵与鉑粉所促成的無机反應有相似性。柏采留斯把這种作用叫做“催化”,說促成化學反應的試劑具有“催化能力”。他指出在生物体中由普通物質、植物液汁或血而生成的無數种化合物,可能是由類似催化劑的有机体所制成的。1878年,庫恩(Kuhne)把這些有机催化劑叫做“□”或酵素。
1862年,拜特洛(Berthelot)与圣吉勒斯(Pean de St Gilles)發現,如按分子比例將乙基醋酸与水混合,經過几星期之后,乙基醋酸就部分水解而成乙醇与醋酸,變化的速度是遞減的。如果從酒精与酸開始,則化學變化朝反方向進行,最后平衡時的比例是相同的。這些反應很慢,但如有礦酸在場,則几點鐘內即可達到同樣的平衡。這樣酸就成了一种催化劑,而且可以看出,催化劑的功用在于促進兩個方向中任何一個方向的化學反應。從某种意義上說,它的作用,好象滑潤劑對机器所起的作用一樣。1887年,阿累利烏斯(Arrhenius)發現酸類的催化作用与其導電率有關。
气体也有同樣的現象。1880年,狄克遜(Dixon)發現如果氫氧二气很干燥,這兩种气体就不能爆炸而成水气。1794年,富勒姆(Fulhame)夫人已早觀察到這個現象。1902年,貝克(BreretonBaker)指出,如化合進行得很慢并且形成了水,就沒有爆炸現象。阿姆斯特朗(Armstrong)表示,反應自身所形成的水過于純粹,沒有催化作用。据我們所知,還有一些時候,純粹的化學物質也是不起作用的,似乎須有复雜的混合物在場,才能促進變化。有机催化劑或□在生物比學上的重要性將在以后几章內敘述。
十九世紀最后几年發現了几個新的惰性元素。1895年,第三代雷利爵士(third Lord Rayleigh)注意到,從空气得來的氮比從其化合物得來的,密度要大一些,因而導引他和拉姆賽發現了一种惰气,命名為氬。跟著發現的還有氦(參看241頁)、氪、氖与氙,這是四年間從空气里發現的五個新元素。氬現在用于熾熱的充气電燈,氬与氖用于廣告霓虹燈,氖因其紅光具有穿透性,更用于燈塔。和別的天然气一道從加拿大和美國的某些土地里逐出的氦气,過去用來充填飛船上的气球。這些元素在門得列耶夫周期表內形成原子价為零的一族,而在以后要敘述的莫斯利的原子序數表里也有其适當的地位。阿斯頓等人后來對于原子量与同位素所進行的研究使得這些气体在理論上比以前更加重要。
溶液理論
物質在水中或其他液体中可以溶解,這是人所熟知的現象。有些液体,如酒精与水,按任何比例都可互相混合,而有些液体如油与水,一點也不能混合。固体如糖可在水里自由溶解,金屬就不溶解;空气与類似的气体僅少許溶解于水,而氨气与氫氯酸气則大量溶解。
物理變化可与溶解同時發生。溶液的容積可能比溶質和溶劑相加的容積小,而且可能有吸熱和放熱現象。許多中性鹽溶解于水時產生致冷效應,可是也有少數鹽類如氯化鋁溶解時發出熱來。酸類与鹼類也常發熱。
這些反應,經過許多化學家研究。他們認識到這种反應的性質很复雜,其中有混合与化合兩种情形,不過,它們的成分不斷改變(与其他化合物之有一定比例不同)說明其間存在有一些特殊關系。但在十九世紀以前沒有人將溶液現象當作特殊問題。
首先有系統地研究溶解物質的擴散的人是格雷厄姆(ThomasCraham,1805-1869年)。他對于气体擴散的實驗,我們在前章已經說過了。格雷厄姆發現,晶体,如許多鹽類,溶解于水時,常能自由地穿過薄膜,可以比較快地從溶液的一部分擴散到另一部分。但明膠一類不形成晶体的物質,溶解后擴散极其緩慢。格雷厄姆稱第一類物体為凝晶体,第二類為膠体。起初以為膠体必定是有机物,但后來才知道許多無机物如硫化砷,甚至金屬如黃金,經過特殊處理,也可以呈膠体狀態。
伏特電池的發明以及立刻隨之而來的關于溶液電解性質的研究,已經敘述過了。1833年,法拉第指出,使一定電量通過電解液時,總是有一定量的离子在電极上析出。如果我們把電流看作是靠离子的運動而傳遞的,這就意味著每一個原子价相同的离子必定帶著同樣的電荷,這樣單价离子所帶的電荷,就成了自然的單位或電原子。
1859年,希托夫(Hittorf)在這個問題上又前進了一步。他讓電流通過兩個不溶的電极,結果兩個電极附近的溶液就程度不等地稀薄起來。希托夫看出,利用這個事實就可以用實驗方法把异性离子運動的速度加以比較,因發放速度較大的离子的電极必失去較多的電解質。這樣就可以測定兩种异性离子的速度比。
1879年,科爾勞施(Kohlrausch)發明了一個測量電解液電阻的好方法。由于极化作用,直流電是不能使用的,但科爾勞施卻克服了這個困難。他采用了交流電和大面積的海綿狀電极,來減少沉淀物的表面密度。他不用電流計,而用對交流電有反應的電話机來作指示器。在這樣避免了极化作用之后,他發現電解液也服從歐姆定律,即電流与電動力成比例。因此最小的電動力也可以使電解質中產生相應的電流;除了在電极附近之外,也沒有极化的反作用。所以离子必定可以自由交換,象克勞胥斯所說的那樣。
科爾勞施就這樣測定了電解質的傳導率,并且指出由于電流為反向离子流所傳送,傳導率一定可以用來測量反向离子速度的總和。再加上希托夫的測定离子速度之比的方法,我們就可以計算個別离子的速度了。在每厘米有1伏特電位差的梯度下,氫在水里運動的速度為每秒0.003厘米,而中性鹽類的离子的速度則約為每秒0.0006厘米。氫离子的速度值,經洛治(Oliver Lodge)爵士在實驗中加以證實。他用一种對氫靈敏的指示劑給明膠著色,使氫离子通過其中,然后加以追跡。中性鹽离子的數值,則為本書作者所證實(本書作者觀察了它們在著色鹽類中的運動),從沉淀的形成中也可以得到證實。這些方法以后又由馬森(Masson)、斯蒂爾(Steele)、麥金尼斯(Maclnnes)等研究者加以改進。
荷蘭物理學家范特-霍夫對于溶液有另外一种看法。我們早已知道,經過細胞膜而滲入植物細胞的水,可以產生一种壓力,植物學家佩弗(Pfeffer)用人工薄膜,即在無釉陶器上用化學方法造成沉淀而制成的薄膜,量度過這种滲透壓。范特-霍夫指出,佩弗的測量表明,滲透壓和其他因素的關系很象气体的壓力,即与容積成反比,并隨絕對溫度而增加。在溶液不能滲透的薄膜中,水或其他溶劑可以進行可逆的滲透的現象使我們可以設想具有滲透性的細胞就是一個理想机器的汽缸,因此,范特-霍夫可以把熱力學的推理應用到溶液上去,從而開辟了一個新的研究領域。他將溶液的滲透壓和其他物理性質如凝固點、汽壓等聯系起來,這樣,通過測量凝固點(這是一項比較容易做的工作),就可以算出滲透壓。他從理論上證明稀溶液的滲透壓的絕對值必与同濃度的气体壓力相同,然后他又用實驗證明了這個結果。我們并不能象有些人所設想的那樣因此就得出推論說;兩种壓力具有相同的原因,或溶解的物質保持著气体狀態。熱力學的推理并不涉及机制的問題,它表明有聯系的量之間的關系,但卻不涉及這种聯系的性質。滲透壓也許象气体的壓力一樣,是由于分子的碰撞而產生的;也許是由于溶質与溶劑之間的化學親合力或化學化合而產生的。不管它的性質怎樣,只要它存在,它就必定适合熱力學原理,在稀溶液中,如范特-霍夫所證明的,它就必定遵循气体定律。可是它的原因未定,至少不是熱力學所能确定的。
1887年,瑞典人阿累利烏斯證明滲透壓与溶液的電解性有關.我們都知道,電解質的滲透壓异常之大,例如氯化鉀或任何類似的二元鹽類的溶液,其壓力為同分子濃度的糖溶液的壓力的兩倍。阿累利烏斯發現,這种特大的壓力不但与電解的導電度有關,并且与化學的活動性,如酸類在糖發酵而變為酒精的過程中的催化能力也有關系。他的結論是這种壓力說明電解質中离子互相离解,因此,舉例來說,在氯化鉀溶液中,雖然有若干中性的KCI分子存在,同時也有鉀离子与氯离子各帶著正電荷与負電荷,成為溶液導電度与化學活動性的來源。溶液越淡,离解的鹽越多,到溶液淡到极度時,液中只有K+离子和CI-离子。有人認為這兩种离子彼此分開,是和溶劑化合在一起的。
科爾勞施、范特-霍夫、阿累利烏斯的工作成了物理化學的龐大的上層大廈的起點。在這座大廈里,熱力學与電學結合起來,使理論的知識不斷地增進,并且愈來愈廣泛地實際應用于工業。不但如此,我們也不要忘記后來有一些偉大的物理學家研究了電在气体中的傳導,建成了現代科學中最有特征性的一個分支,而他們的离子觀念卻是溶液理論給予他們的。
從實驗的觀點來看,直接測定滲透壓是很困難的,但是,美國的莫爾斯(Morse)与怀特尼(Whitney),以及英國的貝克萊(Berke-ley)伯爵与哈特萊(E.G.J.Hartley),卻先后在1901年和1906-1916年間,對高濃度的溶液中的滲透壓進行了直接測定。莫爾斯与他的同事所用的測定方法基本上与佩弗的方法相同,只是在細節上大有改進。貝克萊与哈特萊并沒有觀察溶劑的流入在半滲透的小室里造成的壓力,而是使溶液受到逐漸增長的壓力,直到溶劑掉轉運動的方向被排擠出去。他們把所得的結果和范·德·瓦爾斯方程式(見232頁)加以比較;就蔗糖与葡萄糖而言,發現与下列公式最符合:
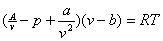
奧斯特瓦爾德(ostwald)把質量作用的化學定律(245頁)應用于阿累利烏斯所想象的電解質的离解,找到一個稀化定律:
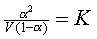
式內α代表電离度,V代表溶液的容積,K是常數。這個方程式對于弱的電解質有效,如輕度离解的酸和鹽,這時上式變為
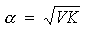
但此式對于高度离解的電解質無效,這一失敗,有很長時間成為電离理論不能為人接受的一個障礙。
這個困難為最近的研究大体上克服。1923-1927年間,德拜(Debxe)、尤格爾(Huckel)与翁薩格(onsager)指出,由于离子間的作用力,离子周圍形成一种异性的离子大气。离子運動時,它須在前面建起一個新的大气,而其背后的大气消散。這一作用形成一种阻擋的電拖曳,使它的運動,与其濃度的平方根成比例而減少。這樣就導出一個相當复雜的方程式。如將离子的可能的締合一并計入,這個方程式与實驗而得的關系,即濃度与導電度的關系,大致符合,就是對強電解質濃溶液來說也是如此。
阿累利烏認為強電解質只有部分离解,而最近的研究卻表明是全部電离。至于濃溶液里相對電离度的減少,那是由于离子速度的變緩的緣故。用X射線分析,表明原子就是在固態的晶体內,也是彼此离開,以后,也有人提出這樣的看法(見384,427-8等頁)。
------------------
素心學苑 收集整理
前一頁
回目錄